
بعض الاساسيات الرياضية في الفيزياء
 المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
 المصدر:
علم البلورات والاشعة السينية
المصدر:
علم البلورات والاشعة السينية
 الجزء والصفحة:
ص46–51
الجزء والصفحة:
ص46–51
 2023-09-19
2023-09-19
 1894
1894
أ - الكميات القياسية Scalars
وهي كميات يكفي لتعيينها معرفة مقدارها دون الحاجة لمعرفة اتجاهها. ومن أمثلتها كثافة جسم ما ودرجة حرارته. إن الكمية القياسية قد تسمى – من منظور عام – كمية ممتدة (أو ممتد) من الرتبة الصفرية.
ب - المتجهات Vectors
وهي الكميات التي تحتاج في تعريفها إلى وجود مقدار واتجاه. ومن أمثلتها الشائعة القوة وهي تمثل بيانيا بسهم ذي طول محدد ويشير رأس السهم إلى الاتجاه المطلوب.
ومن الأمثلة أيضا. شدة المجال الكهربائي في نقطة ما وعزم ثنائي القطب المغناطيسي والميل الحراري في نقطة ما.
ولكل متجه ثلاث مركبات تتخذ اتجاه محاور الإحداثيات الكارتيزية المتعامدة. وتكتب شدة المجال الكهربائي – مثلا – كما يلي:
E = [E1, E2, E3]
وقد يطلق على المتجه مصطلح كمية ممتدة (أو ممتد) من الرتبة الأولى ويفترض أن يكون القارئ على إلمام بمبادئ تحليل المتجهات البسيطة.
جـ - الكميات الممتدة من الرتبة الثانية
عندما يؤثر مجال كهربائي شدته E على موصل أيزوتروبي (أي لا تعتمد الخاصية فيه على الاتجاه) يخضع لقانون أوم فإن كثافة التيار j تكون موازية لشدة المجال، ويكون مقدار j في تناسب مع مقدار E أي أن:

فإذا اخترنا محاور الإحداثيات Ox3, Ox2, Ox1 (وقد تكتب أحيانا Ox Oz, Oy,) فإن:
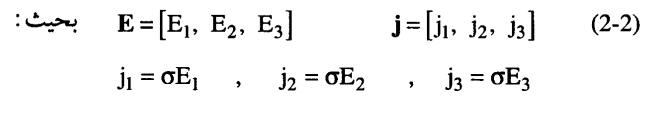
ويختلف الموقف إذا كانت المادة لا أيزوتروبية Anisotropic حيث تكتب المعادلة (2-3) على النحو التالي:
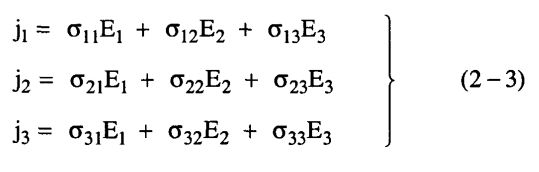
حيث σ11، σ12، ... إلخ ثوابت.
وترتبط كل مركبة من مركبات j خطيا مع مركبات E الثلاث، ومعنى هذا أن j لم تعد موازية لشدة المجال الكهربائي E (الشكل 2-1 ب).
وأصبح لكل من المعاملات σ11، σ12، ... إلخ معنى فيزيائيا. فإذا طبق المجال الكهربائي في اتجاه 1x الشكل (2-1ب) أي:
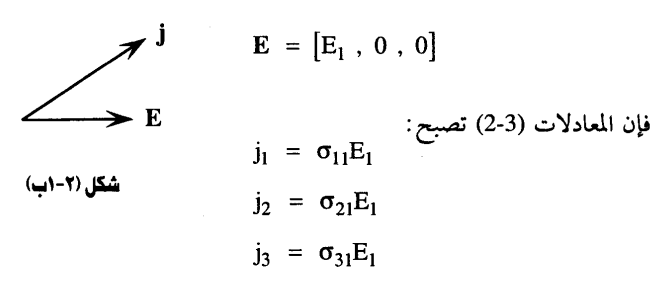
ومعنى هذا أن هناك مركبات لكثافة التيار لا في اتجاه 1x فحسب وإنما في اتجاه المحاور الأخرى. تُعطى المركبة المباشرة بالمعامل σ11 أما المركبتان المستعرضتان فهما σ21، σ31. والمركبة σ23 تعبر – بنفس الطريقة – عن التيار في الموازي للمحور x2 عند تطبيق مجال مواز للمحور x3.
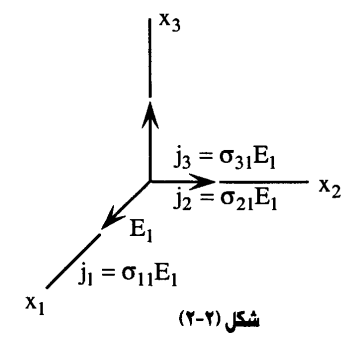
وهكذا يتم التعبير عن موصلية البلورة باستخدام تسعة معاملات σ11، σ12، وتكتب مجتمعة كالتالي:

ويطلق على هذا التكوين كمية ممتدة أو ممتد Tensor من الرتبة الثانية. والكميات ijσ هي مركبات الكمية الممتدة حيث يشير الحرف الأول (i) إلى الصف الذي تقع فيه المركبة ويشير الحرف الثاني (j) إلى العمود وتعرف المركبات 11σ، σ22، σ33 بعناصر قطر الكمية الممتدة.
وهكذا فالكمية الممتدة من الرتبة الصفرية (الكمية القياسية) تعرف برقم مجرد، أما الكمية الممتدة من الرتبة الأولى فتتميز بثلاثة أرقام أو مركبات ترتبط كل منها بأحد المحاور ويكون الممتد من الرتبة الثانية محتويا على تسعة أرقام أو مركبات يرتبط كل منها بزوج من المحاور وتكتب الكميات القياسية بدون رقم سفلي مميز هكذا (الكثافة ρ) أما المتجهات فيميزها رمز بجواره رقم سفلي واحد (مثلا E2) أما مركبات الممتد من الرتبة الثانية فتتميز برقمين سفليين بجوار الرمز (مثلا σ12). أي أن عدد الأرقام السفلية يمكن أن يعتبر مؤشرا على رتبة الكمية الممتدة وامتدادا لهذا الأسلوب يمكننا تعريف الكميات الممتدة من الرتبة الثالثة أو الرابعة أو الأكثر من ذلك.
ويبين الجدول (1-2) بعض أمثلة الكميات الممتدة من الرتبة الثانية التي تربط بين متجهين.
جدول (1-2)
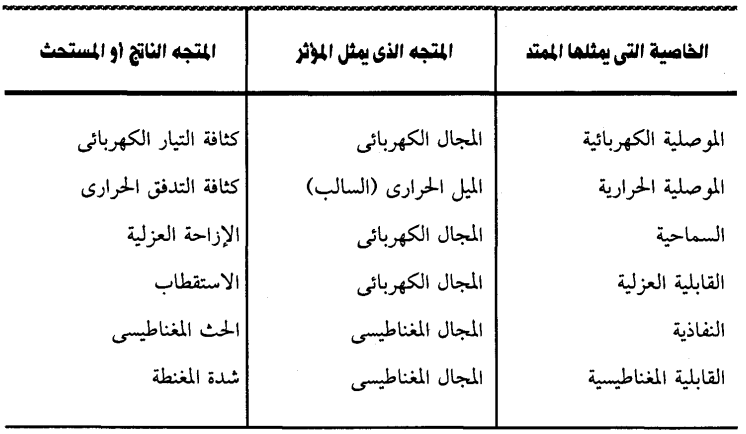
وعلى وجه العموم فإن خاصية ما T تربط بين متجهين [3p، 3p، 1p] = p و [3q، 3q، 1q] = q يمكن أن تكتب هكذا:
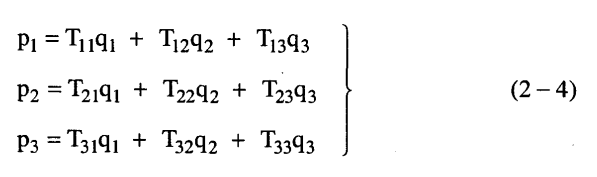
والمعاملات 11T، T12 هي مكونات الكمية الممتدة من الرتبة الثانية.

ويمكن كتابة المعادلة (4-2) بصورة موجزة هكذا:

المعادلة (6-2) خاصة كما علمنا بالبلورات اللا أيزوتروبية، أما في حالة الأجسام الأيزوتروبية فإنها تصبح:

ويكون T مجرد ثابت منفرد.
 الاكثر قراءة في الفيزياء الرياضية
الاكثر قراءة في الفيزياء الرياضية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


