


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | طرق حل مسائل البرمجة الخطية بواسطة طريقة السمبلكس Simplex Method :أمثلة تطبيقية: |
|
|
|
أقرأ أيضاً
التاريخ: 22-2-2022
التاريخ: 29-1-2022
التاريخ: 30-1-2022
التاريخ: 29-1-2022
|
طرق حل مسائل البرمجة الخطية بواسطة طريقة السمبلكس Simplex Method :أمثلة تطبيقية:
مثال 1: إذا اعتبرنا المعادلتين التاليتين. فأوجد الحل الابتدائي للمتغيرات

إذا أضفنا المتغير الفارق (Slack variable)، فيمكن كتابة المعادلات على النحو الآتي:

ويمكن معاملة المعادلات التي تحتوي على أكبر من (2) بواسطة إضافة المتغير الصناعي الفائض (artificial variable) حيث أن المتغير الصناعي لا توجد له أي قيمة طبيعية أو معنوية والغرض من إضافته الحصول الفوري على حل ابتدائي وبعدها تبدأ طريقة السمبلكس التي سوف توضح فيها بعد:

يمكن كتابتها على الصورة: (5.13)

أما في حالة

للحصول على حل ابتدائي وذلك بإضافة المتغير الصناعي فقط:

والامثلة الاتية يمكن ان تعطي توضيح اكثر.
مثال 2:
حول المعادلات الاتية إلى صورة جاهزة لاستخدامها للحل بطريقة السمبلكس.

الحل:

طبقاً للخطوات السابقة ووفقاً للمعادلة فإن الحل الابتدائي:

2- أثر تحميل المعادلات على دالة الهدف:
إن اختيار المتغيرات التي يتخذ عليها القرار يؤثر مباشرة على قيمة دالة الهدف وهذا ينطبق سواء على إضافة (slack variable) او المتغير الصناعي
(artificial variable)
عليه فإن أي دالة يضاف إليها هذين النوعين من المتغيرات سوف تعاد كتابتها على النحو الاتي:

نلاحظ ان الجزء ci xi هو دالة الهدف الاصلية.
أما الجزء c5 x5 هو اثر إضافة على دالة الهدف.
أما الجزء الثالث CA XA فهو أثر إضافة المتغير الصناعي على دالة الهدف.
مثال3:
إذا أعطيت مسألة البرمجة الخطية التالية. المطلوب تغييرها على صيغة قابلة للحل بطريقة السمبلكس.
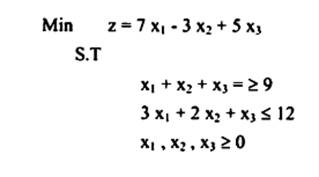
الحل:
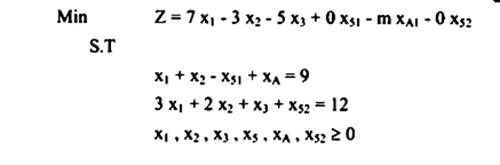
ويمكن صياغة هذه المسألة بصورة أسهل استعمالاً

حيث:
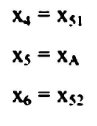
3- بعض التعريفات والرموز المهمة لطريقة السمبلكس :
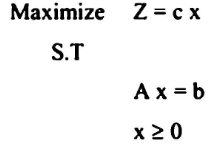
حيث c مصفوفة الصف الواحد (n x 1)
A مصفوفة m x n
B مصفوفة عمود واحد (1 x m )
مثال 4 :
إذا اعتبرنا مسألة البرمجة الخطية التالية حيث:
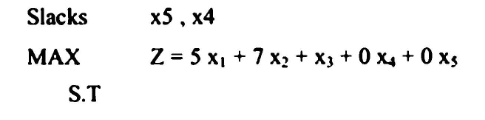

هذه المسألة يمكن كتابتها على النحو التالي:

أي مصفوفة B تسمى حل ابتدائي إذا حققت حل المعادلة A x = b مع الأخذ في الاعتبار ان قيم لـ  وإذا خالف هذا الشرط يسمى حل غير منظور.
وإذا خالف هذا الشرط يسمى حل غير منظور.
أي ان 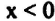
الحل الابتدائي لأي مسألة برمجة خطية

حيث XB
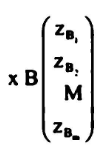
مثال 5 :
في المثال السابق إذا اخترنا
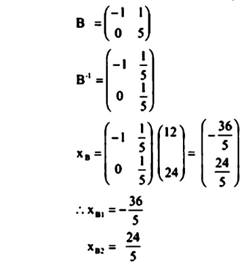
وبما ان 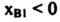
هذا الحل غير منظور



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|