


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | طرق حل مسائل البرمجة الخطية بواسطة طريقة السمبلكس Simplex Method : مقدمة : |
|
|
|
أقرأ أيضاً
التاريخ: 30-1-2022
التاريخ: 27-1-2022
التاريخ: 22-2-2022
التاريخ: 29-1-2022
|
طرق حل مسائل البرمجة الخطية بواسطة طريقة السمبلكس Simplex Method
مقدمة :
إن النظرية الأساسية لحل البرمجة الخطية هي نظرية السمبلكس. وتعتمد هذه النظرية على نظرية نقاط التقاطع (Extreme point theory) وتعتمد فكرة السمبلكس على خلفية واسعة من الجبر الخطي ومن المعروف أنه إذا وجد حل لمسألة البرمجة الخطية فإن المساحة التي تكونها معادلات القيود لابد أن تكون دالة مقعرة (Convex function).
لذلك من المفيد استخدام طريقة السمبلكس في تحديد عدد نقط التقاطع التي أحياناً تكون كبيرة جداً في البحث عن الحل الأمثل.
وعلى سبيل المثال فإن مسالة تحتوي على 20 متغير و 10 قيود يمكن أن يكون لها 48.756 نقطة تقاطع وفقاً للقاعدة:
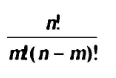
عليه يمكن تلخيص الخطوات الأساسية لطريقة السمبلكس على النحو التالي:
1- البحث أو تحديد نقاط التقاطع بين القيود (النقط الركنة لمنطقة الحل).
2- حساب طريقة الحركة من نقطة لأخرى لتحسين مستوى الحل أو بالأحرى مستوى قيمة دالة الهدف.
3- الاستمرار في النقطة الثانية حتى الوصول إلى الحل الأمثل أو لا حل.
وتتميز هذه الطريقة بقدرتها على التعامل مع عدد كبير من المتغيرات وباعتمادها على جبر المصفوفات بدلاً من الجبر العادي كما يؤدي التتابع في أسلوب الحل إلى الوصول لنتيجة أفضل أو الحل الأمثل.
وبصفة عامة يسهل حل مسائل البرمجة الخطية للمسائل التي تحتوي معادلاتها على ( ) أسهل منها في حالة (=) أو ( ≤) مع شرط أن يكون الطرق الأيمن (bi) موجباً وفي حالة كونه سالباً يجب ضرب المعادلة في إشارة (-) قبل الشروع في الحل.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|