
Lorentz Transformation of Fields
 المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 69
الجزء والصفحة:
part 1 , p 69
 9-8-2016
9-8-2016
 1514
1514
Lorentz Transformation of Fields
a) Write down the Lorentz transformation equations relating the space time coordinates of frames K and K', where K' moves with velocity v relative to K. (Take v to point along a coordinate axis for simplicity.) Explicitly define your 4-vector conventions.
b) Use the fact that the electromagnetic field components E and B form an antisymmetric tensor to show that
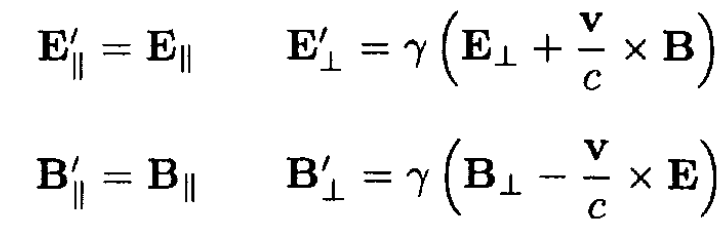
where 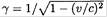 and the subscripts label directions parallel and perpendicular to v.
and the subscripts label directions parallel and perpendicular to v.
c) Consider the particular case of a point charge q and recover an appropriate form of the law of Biot and Savart for small v.
SOLUTION
a) Using a 4-vector of the form
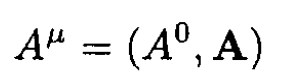 (contravariant form)
(contravariant form)
and recalling that for v pointing along the x-axis, we have for the Lorentz transformation of a 4-vector
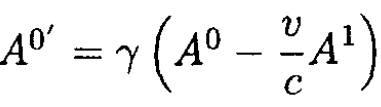 (1)
(1)
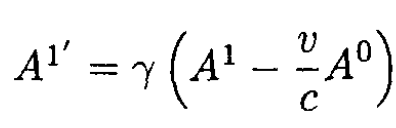 (2)
(2)
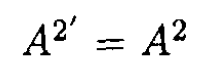 (3)
(3)
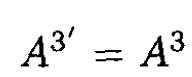
For space–time coordinates,
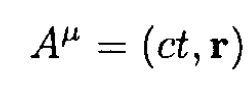
and we have from (1)–(4)
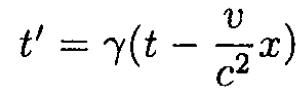 (5)
(5)
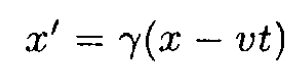 (6)
(6)
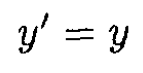 (7)
(7)
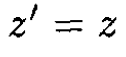 (8)
(8)
b) Writing the explicitly antisymmetric field-strength tensor,
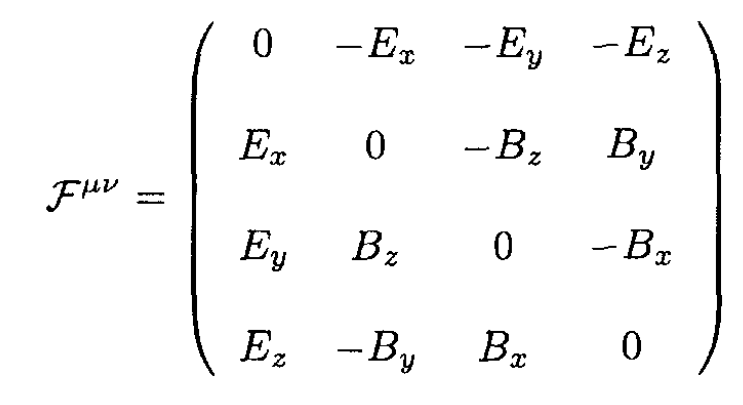 (9)
(9)
where F01 and F23 do not change under the Lorentz transformation and F02, F02 and F12, F13 transform as x0 and x1 respectively.
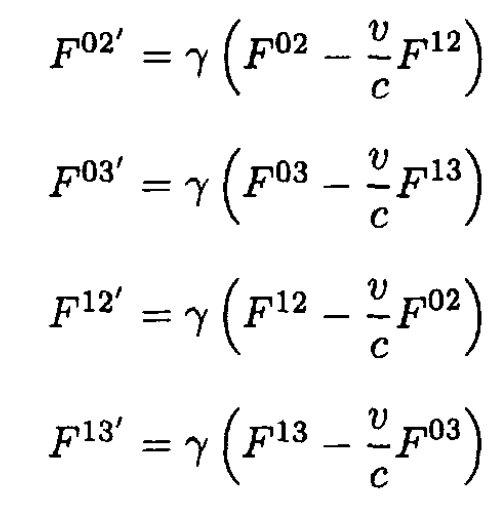 (10)
(10)
Substituting (9) into (10), we obtain
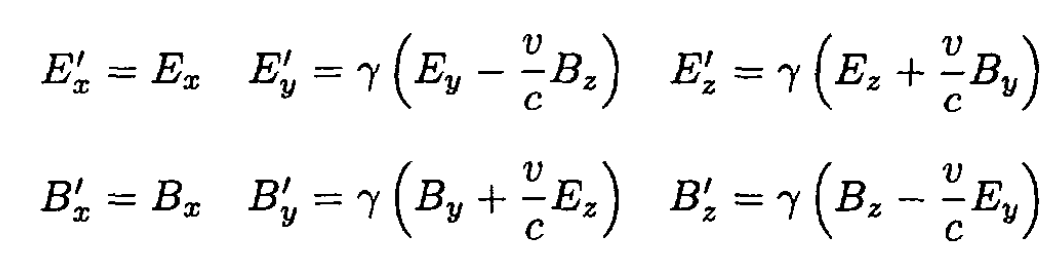 (11)
(11)
We can rewrite (11) is terms of the parallel and perpendicular components of the fields:
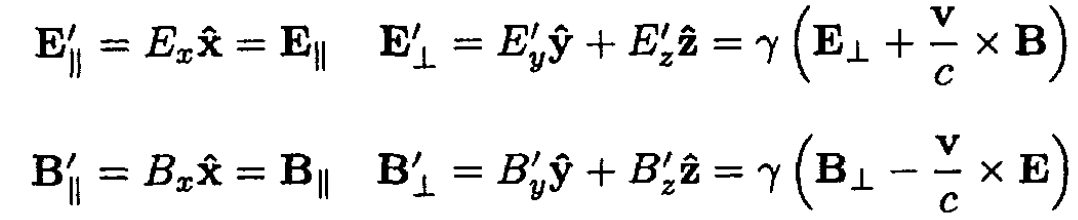 (12)
(12)
c) In the case of a point charge q, we have to transform from K' to K which is equivalent to changing the sign of the velocity in (12). For a small velocity v, we may write
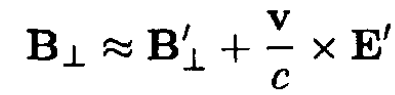
where we have changed the signs in (12) and taken γ ≈ 1. For a point charge in K', B' = 0 and
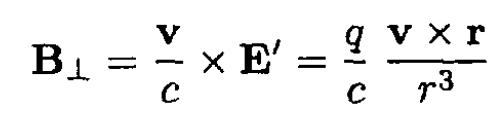
which is the magnetic field for a charge moving with velocity v.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


