Flyball Governor
المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 19
28-7-2016
3062
Flyball Governor
Consider the flyball governor for a steam engine shown in Figure 1.1. Two balls, each of mass m, are attached by means of four hinged arms, each of length l, to sleeves on a vertical rod. The upper sleeve is fastened to the rod; the lower sleeve has mass M and is free to slide up and down the rod as the balls move out from or in toward the rod. The rod-and-ball system rotates with constant angular velocity ω.
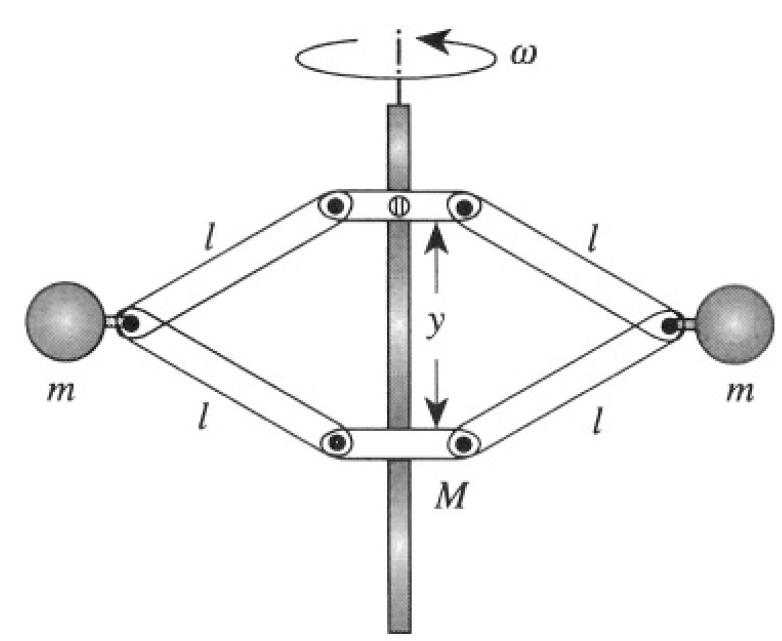
Figure 1.1
a) Set up the equation of motion, neglecting the weight of the arms and rod. Use as variable the distance y between the sleeves.
b) Show that, for steady rotation of the balls, and ω2l/g > (1+ M/m), the value of the height z of the lower sleeve above its lowest point is
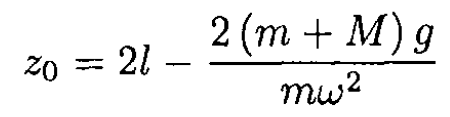
c) Show that the angular frequency Ω of small oscillations of z about the steady value z0 is
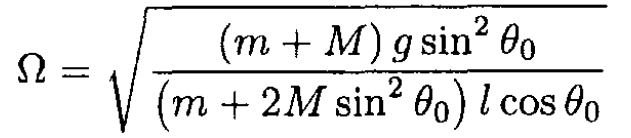
With
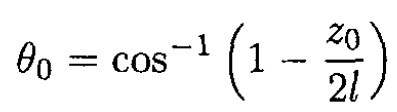
SOLUTION
a) Find the Lagrangian of the system. The kinetic energy
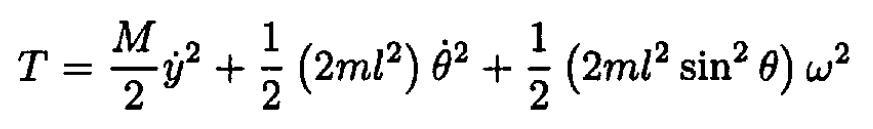(1)
where is the distance of the sleeves from each other and θ is the angle of the hinged rods to the fixed vertical rod (see Figure 1.2). The potential energy
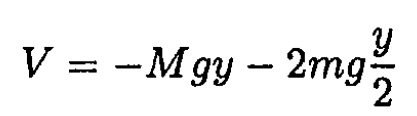(2)
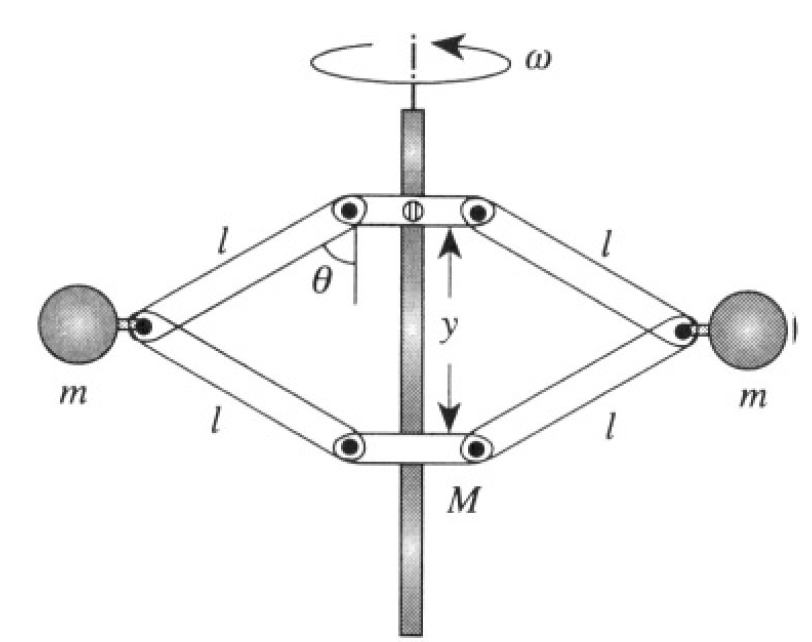
Figure 1.2
Using the relation y = 2lcos θ we obtain for θ ≠ 0
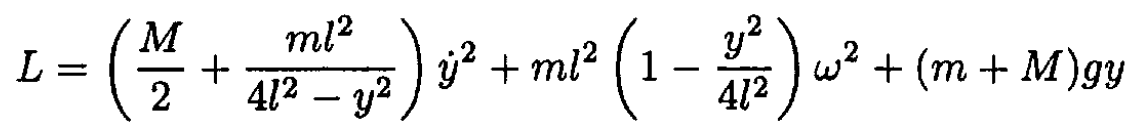(3)
The equation of motion becomes
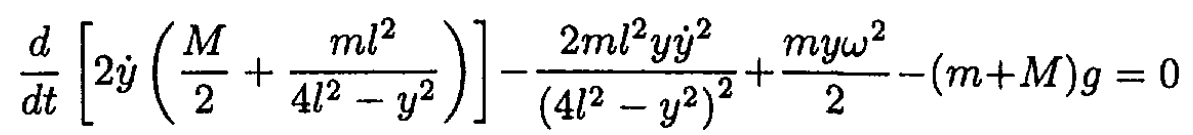(4)
b) From (3), we may introduce the effective potential energy
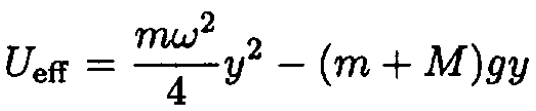(5)
Its minimum gives the equilibrium position of the sleeve y0
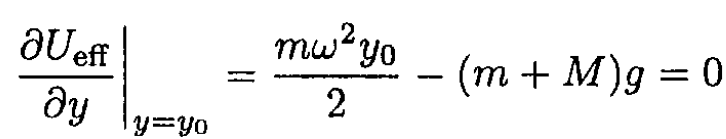(6)
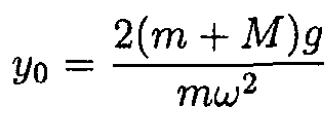(7)
The angle θ corresponding to (7) is defined by
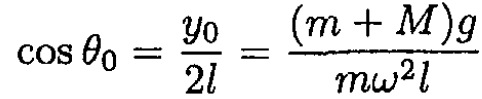(8)
The condition for stability of the equilibrium of (8) is equivalent to
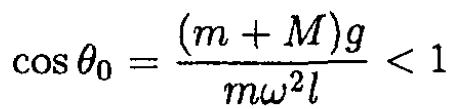(9)
which can clearly be seen if we write everything in terms of θ and not y. On the other hand, if
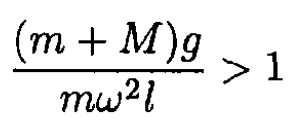
(7) and (8) are no longer valid, and y0 = 2l. This corresponds to the stable equilibrium at θ = 0. So the height z0 of the lower sleeve above its lowest point is
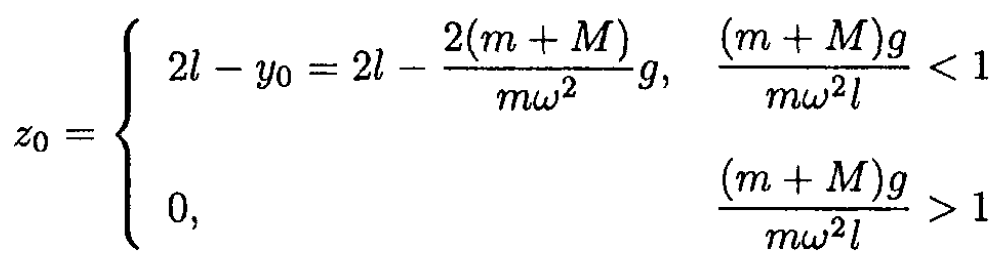(10)
c) Taking the time derivative in (4), we obtain
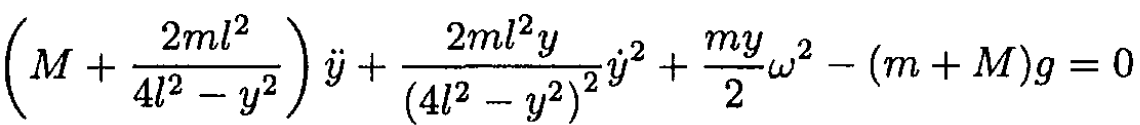(11)
For small oscillations around the equilibrium point y = y0 + η, the quadratic terms of η may be neglected, and we rewrite (11), where y0 is defined in (10) under the conditions in (9)
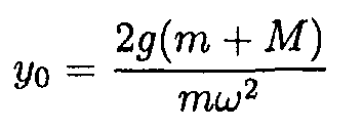(12)
So
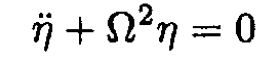(13)
Where Ω is the angular frequency of a simple harmonic oscillator given by
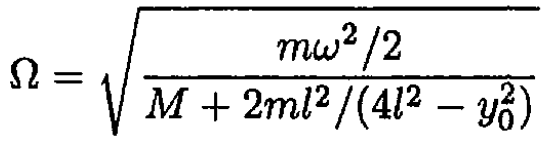(14)
Now, y0 = 2l cos θ0, and using (9), we eliminate ω2 to arrive at
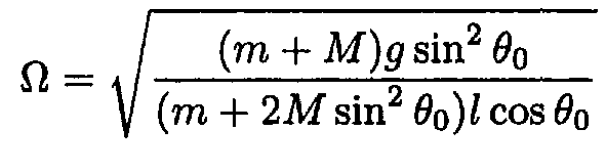(15)
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
