


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-12-2021
Date: 2-1-2022
Date: 11-1-2022
|
Two totally ordered sets 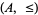 and
and 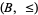 are order isomorphic iff there is a bijection
are order isomorphic iff there is a bijection 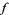 from
from 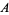 to
to 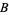 such that for all
such that for all 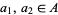 ,
,
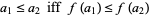 |
(Ciesielski 1997, p. 38). In other words, 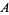 and
and 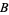 are equipollent ("the same size") and there is an order preserving mapping between the two.
are equipollent ("the same size") and there is an order preserving mapping between the two.
Dauben (1990) and Suppes (1972) call this property "similar." The definition works equally well on partially ordered sets.
REFERENCES:
Ciesielski, K. Set Theory for the Working Mathematician. Cambridge, England: Cambridge University Press, 1997.
Dauben, J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1990.
Mansour, T. "Permutations Avoiding a Pattern from 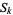 and at Least Two Patterns from
and at Least Two Patterns from 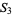 ." 31 Jul 2000. http://arxiv.org/abs/math.CO/0007194.
." 31 Jul 2000. http://arxiv.org/abs/math.CO/0007194.
Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|