


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-12-2021
Date: 14-2-2017
Date: 14-2-2017
|
Let 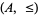 and
and 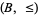 be totally ordered sets. Let
be totally ordered sets. Let 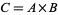 be the Cartesian product and define order as follows. For any
be the Cartesian product and define order as follows. For any 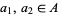 and
and 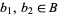 ,
,
1. If 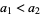 , then
, then 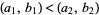 ,
,
2. If 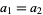 , then
, then 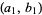 and
and 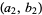 compare the same way as
compare the same way as 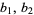 (i.e., lexicographical order)
(i.e., lexicographical order)
(Ciesielski 1997, p. 48; Rubin 1967; Suppes 1972). However, Dauben (1990, p. 104) and Moore (1982, p. 40) define multiplication in the reverse order.
Like addition, multiplication is not commutative, but it is associative,
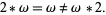 |
(1) |
An inductive definition for ordinal multiplication states that for any ordinal number 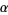 ,
,
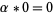 |
(2) |
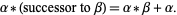 |
(3) |
If 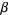 is a limit ordinal, then
is a limit ordinal, then 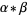 is the least ordinal greater than any ordinal in the set
is the least ordinal greater than any ordinal in the set 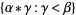 (Suppes 1972, p. 212).
(Suppes 1972, p. 212).
REFERENCES:
Ciesielski, K. Set Theory for the Working Mathematician. Cambridge, England: Cambridge University Press, 1997.
Dauben, J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1990.
Moore, G. H. Zermelo's Axiom of Choice: Its Origin, Development, and Influence. New York: Springer-Verlag, 1982.
Rubin, J. E. Set Theory for the Mathematician. New York: Holden-Day, 1967.
Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مستشفى العتبة العباسية الميداني في سوريا يقدّم خدماته لنحو 1500 نازح لبناني يوميًا
|
|
|