
Functions-Inverse Functions and Permutations
 المؤلف:
Ivo Düntsch and Günther Gediga
المؤلف:
Ivo Düntsch and Günther Gediga
 المصدر:
Sets, Relations, Functions
المصدر:
Sets, Relations, Functions
 الجزء والصفحة:
42-44
الجزء والصفحة:
42-44
 14-2-2017
14-2-2017
 2303
2303
Recall Definition 1.3in( One–one, Onto, and Bijective Functions) of the converse R˘ of a relation R on a set A;
we have obtained the converse R˘ of R by turning around all the arrows, resp. the order of the components. This was always possible, since a relation was just a set of ordered pairs with no other conditions attached.
For a function, reversing the arrows need not result in another function: Consider the examples in Figure 1.1in ( One–one, Onto, and Bijective Functions) . In the surjective function, turning around the arrows does not result in a function, because there are two arrows leaving e.
Furthermore, you will notice that applying f to an element of dom f and then applying g to the result gets us right back to where we started, in other words, g(f(a)) = a. This property is decisive, and leads to the following
Definition 1.1. Let f : A → B and g : B → A be functions; g is called the inverse of f, denoted by f−1 , if g(f(x)) = x for all x ∈ A.
In other words, g is an inverse of f if and only if g ◦ f = idA. The examples above suggest that a function which is not bijective cannot have an inverse. The following Theorem shows that this observation is correct.
Theorem 1.1. f : A → B has an inverse if and only if f is injective.
Proof. “⇒”: Suppose that g : B → A is an inverse of f; we have to show that f is one–one. Let x,y ∈ A and f(x) = f(y); then, g(f(x)) = g(f(y)). Since g is an inverse of f, we have g(f(x)) = x and g(f(y)) = y, which implies x = y.
“⇐”: Suppose that f : A → B is one–one; for each y ∈ B we distinguish two cases:
1. y ∈ ran f: Then there is exactly one x ∈ A such that f(x) = y, since f is one–one. Now set g(y) = x.
2. x ∉ran f: Choose an arbitrary element yx of A, and set g(y) = yx. So, dom g = B, codom g = A, and, since, f is one–one, each element of B is assigned exactly one element of A; hence, g : B → A is a function.
Finally, let x ∈ A; by definition of g we have g(f(x)) = x, which shows that g is an inverse of f.
Note that in case f is one–one but not onto it has more than one inverse function, since g is defined arbitrarily for every x ∈ B which is not in the range of f. Those elements of the codomain which are not in the range of f are in a way immaterial to the assignment f; from previous examples we know that a one–one function can be made bijective by restricting its codomain to the range. If f is bijective then there is only one inverse function:
Theorem 1.2. If f : A → B is bijective, then f has unique inverse g : B → A; furthermore, f is an inverse to g.
Proof. Since f is bijective, it is one–one, and thus it has an inverse g : B → A.
Suppose that h : B → A is also an inverse to f, i.e. we have h(f(x)) = x for every x ∈ A. Since in particular f is onto, for every y ∈ B there is an x ∈ A such that f(x) = y; now, since g is an inverse to f, we have g(y) = g(f(x)) = x, and since h is also an inverse to f, we have h(y) = h(f(x)) = x. It follows that g(y) = h(y) for all y ∈ B, which shows that g = h.
For the second part we have to show that f(g(y)) = y for all y B. Thus, let y ∈ B.
Since f is onto, there exists an x ∈ A such that f(x) = y. Thus,
f(g(y)) = f(g(f(x))) = f(x),
since g is an inverse of f, and hence, g(f(x)) = x.
Let us briefly look at bijective functions f : A → A, where A is a finite set.
Definition 1.2. Let A = {1, 2, 3,. . ., n}, and f : A → A be a bijective function;
then f is called a permutation on n.
The reason for calling these function permutations is that they arrange (i.e. permute) the elements of Ain a different order. Amore general definition of a permutation would allow as domain arbitrary finite sets. For example, if you have n books arranged on a shelf and you put them in a different order, you have in fact performed a permutation of n objects.
If n is small there is a convenient way of picturing f; for example if A = {1, 2, 3, 4, 5}, and f(1) = 1, f(2) = 3, f(3) = 5, f(4) = 2, f(5) = 4, then we can write

Observe that every element of A appears exactly once in each of the two lines, since f is bijective. In general, if A = {1, 2,. . ., n}, and f(1) = a1,f(2) = a2,. . ., f(n) = an, we can list the function by

It is easy to find the inverse of a permutation by just looking from bottom to top in the given list. Let us go back to the example above: The inverse g of f looks like this:

This method of representing a permutation is also useful for obtaining the composition; look at the following two permutations of A:
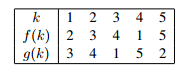
By going through the tables, we find that for h = g ◦ f,
 الاكثر قراءة في نظرية المجموعات
الاكثر قراءة في نظرية المجموعات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


