


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-2-2016
Date: 4-1-2022
Date: 5-1-2022
|
Let 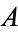 and
and 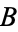 be any sets, and let
be any sets, and let 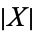 be the cardinal number of a set
be the cardinal number of a set 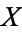 . Then cardinal exponentiation is defined by
. Then cardinal exponentiation is defined by
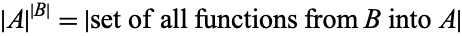 |
(Ciesielski 1997, p. 68; Dauben 1990, p. 174; Moore 1982, p. 37; Rubin 1967, p. 275, Suppes 1972, p. 116).
It is easy to show that the cardinal number of the power set of 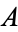 is
is 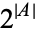 , since
, since 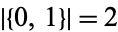 and there is a natural bijection between the subsets of
and there is a natural bijection between the subsets of 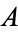 and the functions from
and the functions from 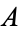 into
into 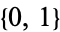 .
.
REFERENCES:
Ciesielski, K. Set Theory for the Working Mathematician. Cambridge, England: Cambridge University Press, 1997.
Dauben, J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1990.
Moore, G. H. Zermelo's Axiom of Choice: Its Origin, Development, and Influence. New York: Springer-Verlag, 1982.
Rubin, J. E. Set Theory for the Mathematician. New York: Holden-Day, 1967.
Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|