Graham's Biggest Little Hexagon

Graham's biggest little hexagon is the largest possible (not necessarily regular) convex hexagon with polygon diameter 1 (i.e., for which no two of the vertices are more than unit distance apart). It is therefore the biggest little polygon for the case 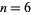. The solution is given by the above figure (which is shown with incorrect proportions in Conway and Guy 1996, p. 207), in which the red lines are all diagonals of unit length.

To find the hexagon, set up coordinates as illustrated above, then the polygon area formula gives

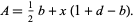(1)

Plugging in together with

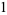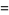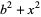			(2)
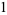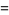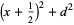			(3)

and eliminating 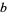 and 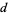 then gives the formula for  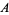as

(4)

This function is plotted above.

Maximizing gives the area of the hexagon as the second-largest real root of

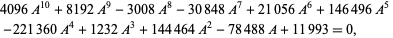(5)

approximately given by 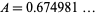 (OEIS A111969). Note that the sign of the  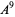is positive, not negative as erroneously given in Conway and Guy (1996). Also compare this with the area of the regular hexagon of diameter 1 (and therefore having circumradius 1/2), which is given by

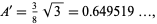(6)

so the optimal solution is 3.9% larger.

The values of  and 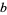 corresponding to the maximal solution are given by

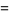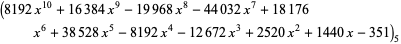			(7)
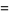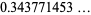			(8)
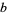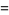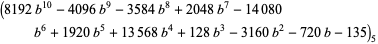			(9)
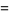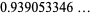			(10)

(OEIS A111970 and A111971).

REFERENCES:

Audet, C.; Hansen, P.; Messine, F.; and Xiong, J. "The Largest Small Octagon." J. Combin. Th. Ser. A 98, 46-59, 2002.

Audet, C.; Hansen, P.; Messine, F.; and Perron, S. "The Minimum Diameter Octagon with Unit-Length Sides: Vincze's Wife's Octagon is Suboptimal." J. Combin. Th. Ser. A 108, 63-75, 2004.

Conway, J. H. and Guy, R. K. "Graham's Biggest Little Hexagon." In The Book of Numbers. New York: Springer-Verlag, pp. 206-207, 1996.

Graham, R. L. "The Largest Small Hexagon." J. Combin. Th. Ser. A 18, 165-170, 1975.

Klein, A. and Wessler, M. "The Largest Small Polytopes." 19 Dec 2002. http://arxiv.org/abs/math.CO/0212262.

Sloane, N. J. A. Sequences A111969, A111970, and A111971 in "The On-Line Encyclopedia of Integer Sequences."

Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, pp. 46-47, 2006. http://www.mathematicaguidebooks.org/.