


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-12-2021
Date: 7-12-2021
Date: 9-12-2021
|
Two families of equations used to find roots of nonlinear functions of a single variable. The "B" family is more robust and can be used in the neighborhood of degenerate multiple roots while still providing a guaranteed convergence rate. Almost all other root-finding methods can be considered as special cases of Schröder's method. Householder humorously claimed that papers on root-finding could be evaluated quickly by looking for a citation of Schröder's paper; if the reference were missing, the paper probably consisted of a rediscovery of a result due to Schröder (Stewart 1993).
One version of the "A" method is obtained by applying Newton's method to 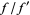 ,
,
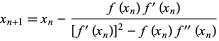 |
(Scavo and Thoo 1995).
REFERENCES:
Householder, A. S. The Numerical Treatment of a Single Nonlinear Equation. New York: McGraw-Hill, 1970.
Scavo, T. R. and Thoo, J. B. "On the Geometry of Halley's Method." Amer. Math. Monthly 102, 417-426, 1995.
Schröder, E. "Über unendlich viele Algorithmen zur Auflösung der Gleichungen." Math. Ann. 2, 317-365, 1870.
Stewart, G. W. "On Infinitely Many Algorithms for Solving Equations." English translation of Schröder's original paper. College Park, MD: University of Maryland, Institute for Advanced Computer Studies, Department of Computer Science, 1993. http://citeseer.nj.nec.com/93609.html.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|