
Wynn,s Epsilon Method
 المؤلف:
Brezinski, C
المؤلف:
Brezinski, C
 المصدر:
"Convergence Acceleration During the 20th Century." J. Comput. Appl. Math. 122
المصدر:
"Convergence Acceleration During the 20th Century." J. Comput. Appl. Math. 122
 الجزء والصفحة:
...
الجزء والصفحة:
...
 9-12-2021
9-12-2021
 1520
1520
Wynn's Epsilon Method
Wynn's 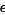 -method is a method for numerical evaluation of sums and products that samples a number of additional terms in the series and then tries to extrapolate them by fitting them to a polynomial multiplied by a decaying exponential.
-method is a method for numerical evaluation of sums and products that samples a number of additional terms in the series and then tries to extrapolate them by fitting them to a polynomial multiplied by a decaying exponential.
In particular, the method provides an efficient algorithm for implementing transformations of the form
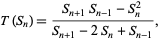 |
(1)
|
where
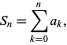 |
(2)
|
is the 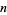 th partial sum of a sequence
th partial sum of a sequence ![<span style=]() {a_k}_(k=0)^infty" src="https://mathworld.wolfram.com/images/equations/WynnsEpsilonMethod/Inline3.gif" style="height:17px; width:42px" />, which are useful for yielding series convergence improvement (Hamming 1986, p. 205). In particular, letting
{a_k}_(k=0)^infty" src="https://mathworld.wolfram.com/images/equations/WynnsEpsilonMethod/Inline3.gif" style="height:17px; width:42px" />, which are useful for yielding series convergence improvement (Hamming 1986, p. 205). In particular, letting 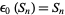 ,
, 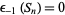 , and
, and
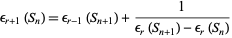 |
(3)
|
for 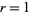 , 2, ... (correcting the typo of Hamming 1986, p. 206). The values of
, 2, ... (correcting the typo of Hamming 1986, p. 206). The values of 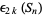 are there equivalent to the results of applying
are there equivalent to the results of applying 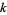 transformations to the sequence
transformations to the sequence 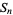 (Hamming 1986, p. 206).
(Hamming 1986, p. 206).
Wynn's epsilon method can be applied to the terms of a series using the Wolfram Language command SequenceLimit[l]. Wynn's method may also be invoked in numerical summation and multiplication using Method -> Fit in the Wolfram Language's NSum and NProduct commands. It is also utilized in the routine NLimit[expr, x -> x0] in the Wolfram Language package NumericalCalculus` .
Wynn's epsilon method is a member of a large family of similar so-called lozenge, or rhombus, transformations (Hamming 1986, p. 207).
REFERENCES:
Brezinski, C. "Convergence Acceleration During the 20th Century." J. Comput. Appl. Math. 122, 1-21, 2000.
Hamming, R. W. Numerical Methods for Scientists and Engineers, 2nd ed. New York: Dover, pp. 206-207, 1986.
Shanks, D. "Nonlinear Transformations of Divergent and Slowly Convergent Sequences." J. Math. Phys. 34, 1-42, 1955.
Weniger, E. J. "Nonlinear Sequence Transformations for the Acceleration of Convergence and the Summation of Divergent Series." 19 Jun 2003. http://arxiv.org/abs/math.NA/0306302.
Wynn, P. "On a Device for Computing the 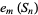 Transformation." Math Tables Aids Comput. 10, 91-96, 1956.
Transformation." Math Tables Aids Comput. 10, 91-96, 1956.
Wynn, P. "Acceleration Techniques in Numerical Analysis, with Particular Reference to Problems in One Independent Variable." Proc. IFIPS, Munich. Munich, pp. 149-156, 1962.
 الاكثر قراءة في التحليل العددي
الاكثر قراءة في التحليل العددي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


