المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Mutual Information |
 1022
 07:41 مساءً
date: 14-11-2021 |
Author : Cover, T. M. and Thomas, J. A 
Book or Source : Elements of Information Theory. New York: Wiley 
Page and Part : pp. 18-26|
Read More
Date: 29-11-2021
1065
Date: 24-11-2021
1021
Date: 25-11-2021
856
|
The mutual information between two discrete random variables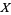 
and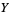 
is defined to be
 |
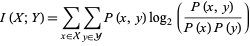(1) |
bits. Additional properties are
 |
 |
 |
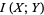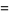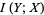(2) |
 |
 |
 |
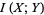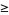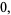(3) |
and
 |
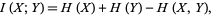(4) |
where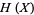 
is the entropy of the random variable 
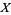and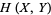 
is the joint entropy of these variables.
REFERENCES:
Cover, T. M. and Thomas, J. A. Elements of Information Theory. New York: Wiley, pp. 18-26, 1991.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
