


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-10-2021
Date: 16-12-2021
Date: 26-8-2021
|
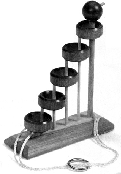
A puzzle involving disentangling a set of rings from a looped double rod, originally used by French peasants to lock chests (Steinhaus 1999). The word "baguenaudier" means "time-waster" in French, and the puzzle is also called the Chinese rings or Devil's needle puzzle. ("Bague" also means "ring," but this appears to be an etymological coincidence. Interestingly, the bladder-senna tree is also known as "baguenaudier" in French.) Culin (1965) attributes the puzzle to Chinese general Hung Ming (A.D. 181-234), who gave it to his wife as a present to occupy her while he was away at the wars.
The solution of the baguenaudier is intimately related to the theory of Gray codes.
The minimum number of moves 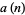 needed for
needed for 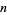 rings is
rings is
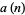 |
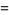 |
![[2/3(2^n-1)]](https://mathworld.wolfram.com/images/equations/Baguenaudier/Inline5.gif) |
(1) |
 |
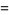 |
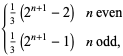 |
(2) |
where ![[x]](https://mathworld.wolfram.com/images/equations/Baguenaudier/Inline9.gif) is the ceiling function, giving 1, 2, 5, 10, 21, 42, 85, 170, 341, 682, ... (OEIS A000975). The generating function for these numbers is
is the ceiling function, giving 1, 2, 5, 10, 21, 42, 85, 170, 341, 682, ... (OEIS A000975). The generating function for these numbers is
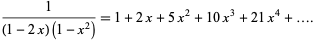 |
(3) |
They are also given by the recurrence relation
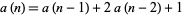 |
(4) |
with 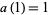 and
and 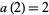 .
.
By simultaneously moving the two end rings, the number of moves for 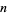 rings can be reduced to
rings can be reduced to
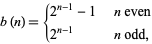 |
(5) |
giving 1, 1, 4, 7, 16, 31, 64, 127, 256, 511, ... (OEIS A051049).
Defining the complexity of a solution as the minimal number of times the ring passes through the arc from the last ring to the base of the puzzle, the minimal complexity of a solution is 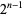 , as conjectured by Kauffman (1996) and proved by Przytycki and Sikora (2000).
, as conjectured by Kauffman (1996) and proved by Przytycki and Sikora (2000).
REFERENCES:
Culin, S. "Ryou-Kaik-Tjyo--Delay Guest Instrument (Ring Puzzle)." §20 in Games of the Orient: Korea, China, Japan. Rutland, VT: Charles E. Tuttle, pp. 31-32, 1965.
Dubrovsky, V. "Nesting Puzzles, Part II: Chinese Rings Produce a Chinese Monster." Quantum 6, 61-65 (Mar.) and 58-59 (Apr.), 1996.
Elliott Avedon Museum and Archive of Games, University of Waterloo, Ontario, Canada. "Wire and Ring Puzzles." http://www.ahs.uwaterloo.ca/~museum/puzzles/wire/.
Gardner, M. "The Binary Gray Code." In Knotted Doughnuts and Other Mathematical Entertainments. New York: W. H. Freeman, pp. 15-17, 1986.
Kauffman, L. H. "Tangle Complexity and the Topology of the Chinese Rings." In Mathematical Approaches to Biomolecular Structure and Dynamics. New York: Springer-Verlag, pp. 1-10, 1996.
Kraitchik, M. "Chinese Rings." §3.12.3 in Mathematical Recreations. New York: W. W. Norton, pp. 89-91, 1942.
Przytycki, J. H. and Sikora, A. S. "Topological Insights from the Chinese Rings." 21 Jul 2000. http://arxiv.org/abs/math.GT/0007134.
Sloane, N. J. A. Sequences A000975 and A051049 in "The On-Line Encyclopedia of Integer Sequences."
Slocum, J. and Botermans, J. Puzzles Old and New: How to Make and Solve Them. Seattle, WA: University of Washington Press, p. 105, 1988.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 268-269, 1999.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|