


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-1-2016
Date: 5-11-2021
Date: 16-8-2021
|
In homogeneous coordinates, the first positive quadrant joins 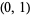 with
with 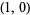 by "points"
by "points" 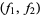 , and is mapped onto the hyperbolic line
, and is mapped onto the hyperbolic line 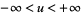 by the correspondence
by the correspondence 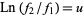 . Now define
. Now define
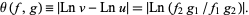 |
(1) |
Let 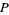 be any bounded linear transformation of a Banach space
be any bounded linear transformation of a Banach space 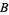 that maps a closed convex cone
that maps a closed convex cone 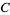 of
of 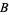 onto itself. Then the
onto itself. Then the 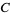 -norm
-norm 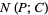 of
of 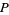 is defined by
is defined by
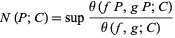 |
(2) |
for pairs 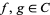 with finite
with finite 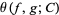 . Birkhoff's inequality then states that if the transform
. Birkhoff's inequality then states that if the transform 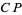 of
of 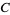 under
under 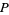 has finite diameter
has finite diameter 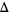 under
under 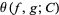 , then
, then
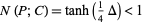 |
(3) |
(Birkhoff 1957).
REFERENCES:
Birkhoff, G. "Extensions of Jentzsch's Theorem." Trans. Amer. Math. Soc. 85, 219-227, 1957.
Jentzsch, R. "Über Integralgleichungen mit positivem Kern." J. reine angew. Math. 141, 235-244, 1912.
Schmeidler, W. Integralgleichungen mit Anwendungen in Physik und Technik, Vol. 1. Lineare Integralgleichungen. Leipzig, Germany: Geest & Portig, p. 298, 1955.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|