


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-9-2021
Date: 18-11-2021
Date: 18-11-2021
|

The Sierpiński carpet is the fractal illustrated above which may be constructed analogously to the Sierpiński sieve, but using squares instead of triangles. It can be constructed using string rewriting beginning with a cell [1] and iterating the rules
![{0->[0 0 0; 0 0 0; 0 0 0],1->[1 1 1; 1 0 1; 1 1 1]}.](https://mathworld.wolfram.com/images/equations/SierpinskiCarpet/NumberedEquation1.gif) |
(1) |
The  th iteration of the Sierpiński carpet is implemented in the Wolfram Language as MengerMesh[n].
th iteration of the Sierpiński carpet is implemented in the Wolfram Language as MengerMesh[n].
Let  be the number of black boxes,
be the number of black boxes,  the length of a side of a white box, and
the length of a side of a white box, and  the fractional area of black boxes after the
the fractional area of black boxes after the  th iteration. Then
th iteration. Then
 |
 |
 |
(2) |
 |
 |
 |
(3) |
 |
 |
 |
(4) |
 |
 |
 |
(5) |
The numbers of black cells after  , 1, 2, ... iterations are therefore 1, 8, 64, 512, 4096, 32768, 262144, ... (OEIS A001018). The capacity dimension is therefore
, 1, 2, ... iterations are therefore 1, 8, 64, 512, 4096, 32768, 262144, ... (OEIS A001018). The capacity dimension is therefore
 |
 |
 |
(6) |
 |
 |
 |
(7) |
 |
 |
 |
(8) |
 |
 |
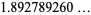 |
(9) |
(OEIS A113210).
REFERENCES:
Allouche, J.-P. and Shallit, J. "The Sierpiński Carpet." §14.1 in Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, pp. 405-407, 2003.
Dickau, R. M. "The Sierpinski Carpet." http://mathforum.org/advanced/robertd/carpet.html.
Gleick, J. Chaos: Making a New Science. New York: Penguin Books, p. 101, 1988.
Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, p. 144, 1983.
Peitgen, H.-O.; Jürgens, H.; and Saupe, D. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, p. 144, 1992.
Reiter, C. A. "Sierpiński Fractals and GCDs." Computers and Graphics 18, 885-891, 1994.
Sierpiński, W. "On Curves Which Contain the Image of Any Given Curve." Mat. Sbornik 30, 267-287, 1916. Reprinted in Oeuvres Choisies, Vol. 2, pp. 107-119.
Sloane, N. J. A. Sequences A001018 and A113210 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
ضمن مؤتمر ذاكرة الألم في العراق دراسة تناقش تجربة المركز العراقي لتوثيق جرائم التطرف وتعاونه مع كراسي اليونسكو في الجامعات العراقية
|
|
|