


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-9-2021
Date: 29-11-2021
Date: 4-11-2021
|

A B-spline is a generalization of the Bézier curve. Let a vector known as the knot vector be defined
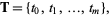 |
(1) |
where 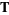 is a nondecreasing sequence with
is a nondecreasing sequence with ![t_i in [0,1]](https://mathworld.wolfram.com/images/equations/B-Spline/Inline2.gif) , and define control points
, and define control points 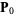 , ...,
, ..., 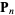 . Define the degree as
. Define the degree as
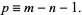 |
(2) |
The "knots" 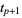 , ...,
, ..., 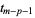 are called internal knots.
are called internal knots.
Define the basis functions as
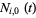 |
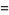 |
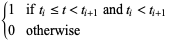 |
(3) |
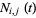 |
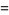 |
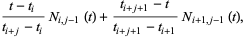 |
(4) |
where 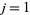 , 2, ...,
, 2, ..., 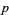 . Then the curve defined by
. Then the curve defined by
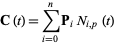 |
(5) |
is a B-spline.
Specific types include the nonperiodic B-spline (first 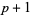 knots equal 0 and last
knots equal 0 and last 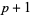 equal to 1; illustrated above) and uniform B-spline (internal knots are equally spaced). A B-spline with no internal knots is a Bézier curve.
equal to 1; illustrated above) and uniform B-spline (internal knots are equally spaced). A B-spline with no internal knots is a Bézier curve.
A curve is 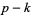 times differentiable at a point where
times differentiable at a point where 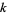 duplicate knot values occur. The knot values determine the extent of the control of the control points.
duplicate knot values occur. The knot values determine the extent of the control of the control points.
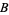 -splines are implemented in the Wolfram Language as BSplineCurve[pts].
-splines are implemented in the Wolfram Language as BSplineCurve[pts].



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|