
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-9-2021
Date: 30-11-2021
Date: 19-11-2021
|

A fractal which can be constructed using string rewriting beginning with a cell [1] and iterating the rules
![{0->[0 1 0; 1 1 1; 0 1 0],1->[1 1 1; 1 1 1; 1 1 1]}.](https://mathworld.wolfram.com/images/equations/CantorSquareFractal/NumberedEquation1.gif) |
(1) |
The size of the unit element after the 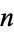 th iteration is
th iteration is
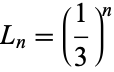 |
(2) |
and the number of elements is given by the recurrence relation
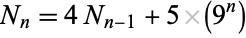 |
(3) |
where 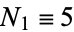 , and the first few numbers of elements are 5, 65, 665, 6305, ... (OEIS A118004). Expanding out gives
, and the first few numbers of elements are 5, 65, 665, 6305, ... (OEIS A118004). Expanding out gives
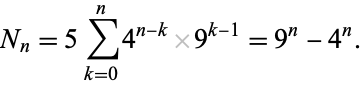 |
(4) |
The capacity dimension is therefore
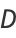 |
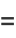 |
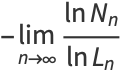 |
(5) |
 |
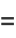 |
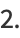 |
(6) |
Since the dimension of the filled part is 2 (i.e., the square is completely filled), Cantor's square fractal is not a true fractal.
REFERENCES:
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 82-83, 1991.
Sloane, N. J. A. Sequence A118004 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|