المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Crookedness |
 2165
 03:40 مساءً
date: 8-6-2021 |
Author : Milnor, J. W. 
Book or Source : "On the Total Curvature of Knots." Ann. Math. 52 
Page and Part : ...|
Read More
Date: 2-7-2017
1666
Date: 20-5-2021
1878
Date: 24-6-2021
1478
|
Let a knot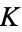 
be parameterized by a vector function 
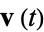with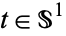 
, and let 
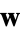be a fixed unit vector in 
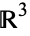. Count the number of local minima of the projection function 
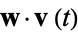. Then the minimum such number over all directions 
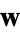and all 
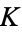of the given type is called the crookedness 
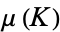. Milnor (1950) showed that 
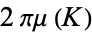is the infimum of the total curvature of 
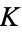. For any tame knot 
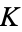in 
, 
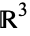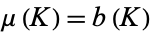where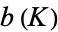 
is the bridge index.
REFERENCES:
Milnor, J. W. "On the Total Curvature of Knots." Ann. Math. 52, 248-257, 1950.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, p. 115, 1976.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
بمساحة 9000 م2 .. العتبة العلوية المقدسة تُنفّذ مشروعًا تربويًّا بتصاميم حديثة ومرافق تعليمية متطوّرة لخدمة آلاف الطلبة
|
|
|
