


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-6-2021
Date: 6-7-2017
Date: 24-7-2021
|
In algebraic topology, the Reidemeister torsion is a notion originally introduced as a topological invariant of 3-manifolds which has now been widely adapted to a variety of contexts. At the time of its discovery, the Reidemeister torsion was the first 3-manifold invariant able to distinguish between manifolds which are homotopy equivalent but not homeomorphic. Since then, the notion has been adapted to higher-dimensional manifolds, knots and links, dynamical systems, Witten's equations, and so on. In particular, it has a number of different definitions for various contexts.
For a commutative ring 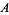 , let
, let 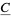 be a finite acyclic chain complex of based finitely generated free R-modules of the form
be a finite acyclic chain complex of based finitely generated free R-modules of the form
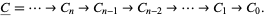 |
(1) |
The Reidemeister torsion of 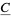 is the value
is the value 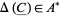 defined by
defined by
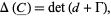 |
(2) |
where 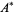 is the set of units of
is the set of units of 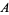 ,
, 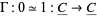 is a chain contraction,
is a chain contraction, 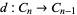 is the boundary map, and
is the boundary map, and
![d+Gamma=[d 0 0 ...; Gamma d 0 ...; 0 Gamma d ...; | | | ...]](https://mathworld.wolfram.com/images/equations/ReidemeisterTorsion/NumberedEquation3.gif) |
(3) |
is a map from 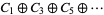 to
to 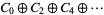 . In this context, Reidemeister torsion is sometimes referred to as the torsion of the complex
. In this context, Reidemeister torsion is sometimes referred to as the torsion of the complex 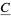 (Nicolaescu 2002) and can be considered a generalization of the determinant of a matrix (Ranicki 1997).
(Nicolaescu 2002) and can be considered a generalization of the determinant of a matrix (Ranicki 1997).
Another common context for which to define Reidemeister torsion is in the case of CW-complexes. Begin with a compact metric space 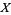 with finite CW-decomposition
with finite CW-decomposition 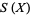 and consider the canonically induced chain complex
and consider the canonically induced chain complex 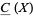 of free Abelian groups,
of free Abelian groups,
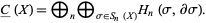 |
(4) |
Lifting 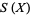 to a CW-decomposition
to a CW-decomposition 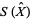 of the maximal Abelian cover
of the maximal Abelian cover 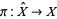 of
of 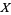 yields an associated chain complex
yields an associated chain complex 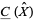 which has a
which has a ![Z[H_1(X)]](https://mathworld.wolfram.com/images/equations/ReidemeisterTorsion/Inline20.gif) basis. In particular, defining
basis. In particular, defining
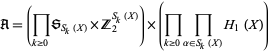 |
(5) |
where 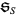 denotes the group of permutations of a set
denotes the group of permutations of a set 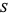 , the torsion of the chain complex
, the torsion of the chain complex 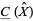 of free
of free ![Z[H_1(X)]](https://mathworld.wolfram.com/images/equations/ReidemeisterTorsion/Inline24.gif) -modules with respect to the
-modules with respect to the 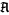 -orbit of
-orbit of ![Z[H_1(X)]](https://mathworld.wolfram.com/images/equations/ReidemeisterTorsion/Inline26.gif) -bases is called the Reidemeister torsion of
-bases is called the Reidemeister torsion of 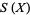 . In this context, the Reidemeister torsion is a well-defined element of
. In this context, the Reidemeister torsion is a well-defined element of ![Q(Z[H_1(X)])/+/-H_1(X)](https://mathworld.wolfram.com/images/equations/ReidemeisterTorsion/Inline28.gif) . In-depth details of this construction can be found in e.g., Nicolaescu (2002).
. In-depth details of this construction can be found in e.g., Nicolaescu (2002).
Reidemeister torsion is sometimes known as R-torsion or Reidemeister-Franz torsion. What's more, R-torsion is closely related to a number of other topological tools including Whitehead torsion, and was proven by Cheeger and Müller to be identically equal to the analytic torsion in the case of compact Riemannian manifolds.
SEE ALSO:Acyclic Chain Complex, Analytic Torsion, Basis, Chain, Chain Complex, Chain Contraction, Chain Homomorphism, Commutative Ring, Compact Manifold, Compact Space, Connected, Covering Space, CW-Complex, Determinant, Dynamical System, Free Abelian Group, Group, Group Generators, Group Orbit, Group Ring, Group Torsion, Homeomorphism, Homotopy Equivalence, Invariant, Knot, Link, Manifold, Metric Space, Module, Permutation Group, Quotient Group, R-Module, Riemannian Manifold, Torsion, Union, Unit, Unit Ring, Vector Basis, Whitehead Torsion, Witten's Equations
REFERENCES:
Cheeger, J. "Analytic Torsion and Reidemeister Torsion." Proc. Natl. Acad. Sci. USA 74, 2651-2654, 1977.
Nicolaescu, L. I. "Notes on the Reidemeister Torsion." 2002. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.8.4031&rep=rep1&type=pdf.
Ranicki, A. "Notes on Reidemeister Torsion." 1997. https://www.maths.ed.ac.uk/~aar/papers/torsion.pdf.
Turaev, V. G. "Reidemeister Torsion in Knot Theory." Uspekhi Mat. Nauk. 41, 97-147, 1986.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|