Point Process

A point process is a probabilistic model for random scatterings of points on some space 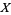 often assumed to be a subset of  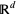for some 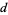. Oftentimes, point processes describe the occurrence over time of random events in which the occurrences are revealed one-by-one as time evolves; in this case, any collection

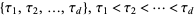of occurrences is said to be a realization of the point process.

Poisson processes are regarded as archetypal examples of point processes (Daley and Vere-Jones 2002).

Point processes are sometimes known as counting processes or random scatters.

REFERENCES:

Brillinger, D. R.; Guttorp, P. M.; and Schoenberg, F. P. "Point Processes, Temporal." Encyclopedia of Environments 3, 1577-1581, 2002.

Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume I: Elementary Theory and Methods, 2nd ed. New York: Springer, 2003.

Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume II: General Theory and Structure, 2nd ed. New York: Springer, 2007.

Jacobsen, M. Point Process Theory and Applications: Marked Point and Piecewise Deterministic Process. Boston: Birkhäuser, 2006.