


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-10-2020
Date: 28-10-2020
Date: 2-1-2020
|
Let 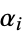 and
and 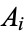 be algebraic numbers such that the
be algebraic numbers such that the 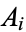 s differ from zero and the
s differ from zero and the 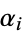 s differ from each other. Then the expression
s differ from each other. Then the expression
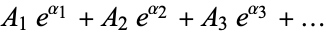 |
cannot equal zero. The theorem was proved by Hermite (1873) in the special case of the 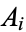 s and
s and 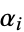 s rational integers, and subsequently proved for algebraic numbers by Lindemann in 1882 (Lindemann 1888). The proof was subsequently simplified by Weierstrass (1885) and Gordan (1893).
s rational integers, and subsequently proved for algebraic numbers by Lindemann in 1882 (Lindemann 1888). The proof was subsequently simplified by Weierstrass (1885) and Gordan (1893).
REFERENCES:
Dörrie, H. "The Hermite-Lindemann Transcendence Theorem." §26 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 128-137, 1965.
Hermite, C. "Sur la fonction exponentielle." Comptes Rendus Acad. Sci. Paris 77, 18-24, 1873.
Gordan, P. "Transcendenz von 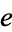 und
und 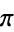 ." Math. Ann. 43, 222-224, 1893.
." Math. Ann. 43, 222-224, 1893.
Lindemann, F. "Über die Ludolph'sche Zahl." Sitzungber. Königl. Preuss. Akad. Wissensch. zu Berlin No. 2, pp. 679-682, 1888.
Weber, H. Lehrbuch der Algebra, Vols. I-II. New York: Chelsea, 1902.
Weierstrass, K. "Zu Hrn. Lindemann's Abhandlung: 'Über die Ludolph'sche Zahl.' " Sitzungber. Königl. Preuss. Akad. Wissensch. zu Berlin No. 2, pp. 1067-1086, 1885.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|