


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-12-2019
Date: 28-5-2020
Date: 3-8-2020
|
There are two different definitions of generalized Fermat numbers, one of which is more general than the other. Ribenboim (1996, pp. 89 and 359-360) defines a generalized Fermat number as a number of the form 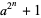 with
with 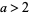 , while Riesel (1994) further generalizes, defining it to be a number of the form
, while Riesel (1994) further generalizes, defining it to be a number of the form 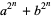 . Both definitions generalize the usual Fermat numbers
. Both definitions generalize the usual Fermat numbers 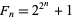 . The following table gives the first few generalized Fermat numbers for various bases
. The following table gives the first few generalized Fermat numbers for various bases 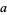 .
.
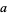 |
OEIS | generalized Fermat numbers in base 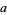 |
| 2 | A000215 | 3, 5, 17, 257, 65537, 4294967297, ... |
| 3 | A059919 | 4, 10, 82, 6562, 43046722, ... |
| 4 | A000215 | 5, 17, 257, 65537, 4294967297, 18446744073709551617, ... |
| 5 | A078303 | 6, 26, 626, 390626, 152587890626, ... |
| 6 | A078304 | 7, 37, 1297, 1679617, 2821109907457, ... |
Generalized Fermat numbers can be prime only for even 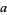 . More specifically, an odd prime
. More specifically, an odd prime 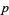 is a generalized Fermat prime iff there exists an integer
is a generalized Fermat prime iff there exists an integer 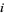 with
with 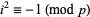 and
and 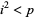 (Broadhurst 2006).
(Broadhurst 2006).
Many of the largest known prime numbers are generalized Fermat numbers. Dubner found 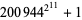 (
(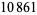 digits) and
digits) and 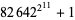 (
(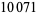 digits) in September 1992 (Ribenboim 1996, p. 360). The largest known as of January 2009 is
digits) in September 1992 (Ribenboim 1996, p. 360). The largest known as of January 2009 is 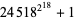 (https://primes.utm.edu/primes/page.php?id=84401), which has
(https://primes.utm.edu/primes/page.php?id=84401), which has 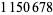 decimal digits.
decimal digits.
The following table gives the first few generalized Fermat primes for various even bases 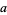 .
.
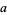 |
prime 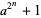 |
| 2 | 5, 17, 257, 65537, ... |
| 4 | 17, 257, 65537, ... |
| 6 | 37, 1297, ... |
REFERENCES:
Broadhurst, D. "GFN Conjecture." Post to primeform user forum. Apr. 1, 2006. https://groups.yahoo.com/group/primeform/message/7187.
Caldwell, C. "The Largest Known Primes." https://primes.utm.edu/primes/lists/all.txt.
Dubner, H. "Generalized Fermat Primes." J. Recr. Math. 18, 279-280, 1985.
Dubner, H. and Keller, W. "Factors of Generalized Fermat Numbers." Math. Comput. 64, 397-405, 1995.
Morimoto, M. "On Prime Numbers of Fermat Type." Sugaku 38, 350-354, 1986.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 102-103 and 415-428, 1994.
Sloane, N. J. A. Sequences A000215/M2503, A059919, A078303, and A078304 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ندوات وأنشطة قرآنية مختلفة يقيمها المجمَع العلمي في محافظتي النجف وكربلاء
|
|
|