


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-1-2020
Date: 10-10-2020
Date: 11-11-2020
|

A polygonal number of the form 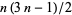 . The first few are 1, 5, 12, 22, 35, 51, 70, ... (OEIS A000326). The generating function for the pentagonal numbers is
. The first few are 1, 5, 12, 22, 35, 51, 70, ... (OEIS A000326). The generating function for the pentagonal numbers is
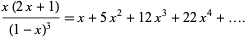 |
Every pentagonal number is 1/3 of a triangular number.
The so-called generalized pentagonal numbers are given by 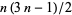 with
with 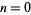 ,
, 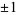 ,
, 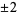 , ..., the first few of which are 0, 1, 2, 5, 7, 12, 15, 22, 26, 35, ... (OEIS A001318).
, ..., the first few of which are 0, 1, 2, 5, 7, 12, 15, 22, 26, 35, ... (OEIS A001318).
There are conjectured to be exactly 210 positive integers that cannot be represented using three pentagonal numbers, namely 4, 8, 9, 16, 19, 20, 21, 26, 30, 31, 33, 38, 42, 43, 50, 54, ..., 20250, 33066, (OEIS A007527; Guy 1994a).
There are six positive integers that cannot be expressed using four pentagonal numbers: 9, 21, 31, 43, 55, and 89 (OEIS A133929).
All positive integers can be expressed using five pentagonal numbers.
Letting 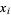 be the set of numbers relatively prime to 6, the generalized pentagonal numbers are given by
be the set of numbers relatively prime to 6, the generalized pentagonal numbers are given by 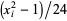 . Also, letting
. Also, letting 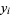 be the subset of the
be the subset of the 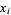 for which
for which 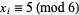 , the usual pentagonal numbers are given by
, the usual pentagonal numbers are given by 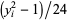 (D. Terr, pers. comm., May 20, 2004).
(D. Terr, pers. comm., May 20, 2004).
REFERENCES:
Guy, R. K. "Every Number Is Expressible as the Sum of How Many Polygonal Numbers?." Amer. Math. Monthly 101, 169-172, 1994a.
Guy, R. K. "Sums of Squares." §C20 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-138, 1994b.
Pappas, T. "Triangular, Square & Pentagonal Numbers." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 214, 1989.
Silverman, J. H. A Friendly Introduction to Number Theory. Englewood Cliffs, NJ: Prentice Hall, 1996.
Sloane, N. J. A. Sequences A000326/M3818, A001318/M1336, A003679/M3323, and A133929 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|