


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-9-2020
Date: 19-11-2020
Date: 3-9-2020
|
A figurate number of the form 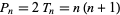 , where
, where 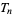 is the
is the 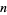 th triangular number. The first few are 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, ... (OEIS A002378). The generating function of the pronic numbers is
th triangular number. The first few are 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, ... (OEIS A002378). The generating function of the pronic numbers is
 |
Kausler (1805) was one of the first to tabulate pronic numbers, creating a list up to 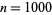 (Dickson 2005, Vol. 1, p. 357; Vol. 2, p. 233).
(Dickson 2005, Vol. 1, p. 357; Vol. 2, p. 233).
Pronic numbers are also known as oblong or heteromecic numbers. However, "pronic" seems to be a misspelling of "promic" (from the Greek promekes, meaning rectangular, oblate, or oblong). However, no less an authority than Euler himself used the term "pronic," so attempting to "correct" it at this late date seems inadvisable.
McDaniel (1998ab) proved that the only pronic Fibonacci numbers are 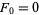 and
and 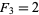 , and the only pronic Lucas number is
, and the only pronic Lucas number is 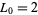 , rediscovering a result first published by Ming (1995).
, rediscovering a result first published by Ming (1995).
The first few 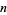 for which
for which 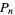 are palindromic are 1, 2, 16, 77, 538, 1621, ... (OEIS A028336), and the first few palindromic numbers which are pronic are 2, 6, 272, 6006, 289982, ... (OEIS A028337).
are palindromic are 1, 2, 16, 77, 538, 1621, ... (OEIS A028336), and the first few palindromic numbers which are pronic are 2, 6, 272, 6006, 289982, ... (OEIS A028337).
REFERENCES:
De Geest, P. "Palindromic Products of Two Consecutive Integers." https://www.worldofnumbers.com/consec.htm.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 357, 2005a.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 6, 232-233, 350, and 407, 2005b.
Euler, L. Republished in Euler, L. Opera Omnia, Ser. 1: Opera mathematica, Vol. 15. Basel, Switzerland: Birkhäuser, 1992.
Guy, R. K. "The Second Strong Law of Small Numbers." Math. Mag 63, 3-20, 1990.
Kausler, C. F. Nova Acta Acad. Petrop. 14, 268-289, ad annos 1797-8, 1805.
McDaniel, W. L. "Pronic Fibonacci Numbers." Fib. Quart. 36, 56-59, 1998a.
McDaniel, W. L. "Pronic Lucas Numbers." Fib. Quart. 36, 60-62, 1998b.
Ming, L. "Nearly Square Numbers in the Fibonacci and Lucas Sequences" [Chinese]. J. Chongqing Teachers College, No. 4, 1-5, 1995.
Sloane, N. J. A. Sequences A002378/M1581, A028336, and A028337 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|