


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-11-2019
Date: 30-12-2020
Date: 23-11-2019
|
Legendre's conjecture asserts that for every 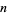 there exists a prime
there exists a prime 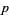 between
between 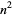 and
and 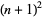 (Hardy and Wright 1979, p. 415; Ribenboim 1996, pp. 397-398). It is one of Landau's problems.
(Hardy and Wright 1979, p. 415; Ribenboim 1996, pp. 397-398). It is one of Landau's problems.
Although it is not known if there always exists a prime 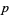 between
between 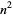 and
and 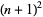 , Chen (1975) has shown that a number
, Chen (1975) has shown that a number 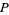 which is either a prime or semiprime does always satisfy this inequality. Moreover, there is always a prime between
which is either a prime or semiprime does always satisfy this inequality. Moreover, there is always a prime between 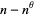 and
and 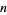 where
where 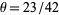 (Iwaniec and Pintz 1984; Hardy and Wright 1979, p. 415).
(Iwaniec and Pintz 1984; Hardy and Wright 1979, p. 415).
The smallest primes between 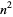 and
and 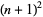 for
for 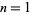 , 2, ..., are 2, 5, 11, 17, 29, 37, 53, 67, 83, ... (OEIS A007491). The numbers of primes between
, 2, ..., are 2, 5, 11, 17, 29, 37, 53, 67, 83, ... (OEIS A007491). The numbers of primes between 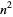 and
and 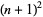 for
for 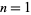 , 2, ... are given by 2, 2, 2, 3, 2, 4, 3, 4, ... (OEIS A014085).
, 2, ... are given by 2, 2, 2, 3, 2, 4, 3, 4, ... (OEIS A014085).
REFERENCES:
Chen, J. R. "On the Distribution of Almost Primes in an Interval." Sci. Sinica 18, 611-627, 1975.
Hardy, G. H. and Wright, W. M. "Unsolved Problems Concerning Primes." §2.8 and Appendix §3 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 19 and 415-416, 1979.
Iwaniec, H. and Pintz, J. "Primes in Short Intervals." Monatsh. f. Math. 98, 115-143, 1984.
Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, pp. 132-134 and 206-208, 1996.
Sloane, N. J. A. Sequences A007491/M1389 and A014085 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تحذير من "عادة" خلال تنظيف اللسان.. خطيرة على القلب
|
|
|
|
|
|
|
دراسة علمية تحذر من علاقات حب "اصطناعية" ؟!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تحذّر من خطورة الحرب الثقافية والأخلاقية التي تستهدف المجتمع الإسلاميّ
|
|
|