
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-12-2019
Date: 19-12-2019
Date: 1-12-2019
|
The heptanacci numbers are a generalization of the Fibonacci numbers defined by  ,
, 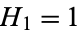 ,
, 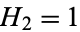 ,
, 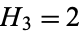 ,
, 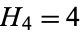 ,
, 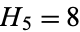 ,
, 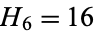 , and the recurrence relation
, and the recurrence relation
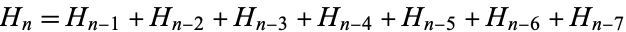 |
(1) |
for 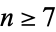 . They represent the
. They represent the 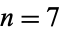 case of the Fibonacci n-step numbers.
case of the Fibonacci n-step numbers.
The first few terms for 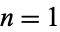 , 2, ... are 1, 1, 2, 4, 8, 16, 32, 64, 127, 253, ... (OEIS A066178).
, 2, ... are 1, 1, 2, 4, 8, 16, 32, 64, 127, 253, ... (OEIS A066178).
An exact formula for the 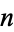 th heptanacci number can be given explicitly in terms of the seven roots
th heptanacci number can be given explicitly in terms of the seven roots 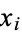 of
of
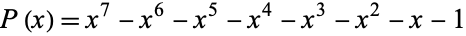 |
(2) |
as
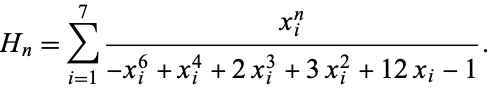 |
(3) |
The ratio of adjacent terms tends to the real root of 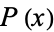 , namely 1.99196419660... (OEIS A118428), sometimes called the heptanacci constant.
, namely 1.99196419660... (OEIS A118428), sometimes called the heptanacci constant.
REFERENCES:
Sloane, N. J. A. Sequence A066178 and A118428 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|