


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-3-2020
Date: 28-7-2020
Date: 27-10-2019
|
A number 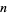 is
is 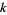 -multiperfect (also called a
-multiperfect (also called a 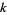 -multiply perfect number or
-multiply perfect number or 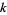 -pluperfect number) if
-pluperfect number) if
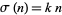 |
for some integer 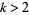 , where
, where 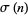 is the divisor function. The value of
is the divisor function. The value of 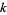 is called the class. The special case
is called the class. The special case 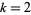 corresponds to perfect numbers
corresponds to perfect numbers 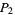 , which are intimately connected with Mersenne primes (OEIS A000396). The number 120 was long known to be 3-multiply perfect (
, which are intimately connected with Mersenne primes (OEIS A000396). The number 120 was long known to be 3-multiply perfect (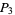 ) since
) since
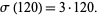 |
The following table gives the first few 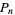 for
for 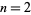 , 3, ..., 6.
, 3, ..., 6.
| 2 | A000396 | 6, 28, 496, 8128, ... |
| 3 | A005820 | 120, 672, 523776, 459818240, 1476304896, 51001180160 |
| 4 | A027687 | 30240, 32760, 2178540, 23569920, ... |
| 5 | A046060 | 14182439040, 31998395520, 518666803200, ... |
| 6 | A046061 | 154345556085770649600, 9186050031556349952000, ... |
Lehmer (1900-1901) proved that 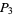 has at least three distinct prime factors,
has at least three distinct prime factors, 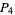 has at least four,
has at least four, 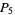 at least six,
at least six, 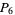 at least nine, and
at least nine, and 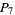 at least 14, etc.
at least 14, etc.
As of 1911, 251 pluperfect numbers were known (Carmichael and Mason 1911). As of 1929, 334 pluperfect numbers were known, many of them found by Poulet. Franqui and García (1953) found 63 additional ones (five 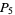 s, 29
s, 29 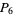 s, and 29
s, and 29 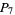 s), several of which were known to Poulet but had not been published, bringing the total to 397. Brown (1954) discovered 110 pluperfects, including 31 discovered but not published by Poulet and 25 previously published by Franqui and García (1953), for a total of 482. Franqui and García (1954) subsequently discovered 57 additional pluperfects (3
s), several of which were known to Poulet but had not been published, bringing the total to 397. Brown (1954) discovered 110 pluperfects, including 31 discovered but not published by Poulet and 25 previously published by Franqui and García (1953), for a total of 482. Franqui and García (1954) subsequently discovered 57 additional pluperfects (3 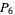 s, 52
s, 52 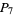 s, and 2
s, and 2 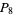 s), increasing the total known to 539.
s), increasing the total known to 539.
An outdated database is maintained by R. Schroeppel, who lists 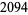 multiperfects, and up-to-date lists by J. L. Moxham and A. Flammenkamp. It is believed that all multiperfect numbers of index 3, 4, 5, 6, and 7 are known. The number of known
multiperfects, and up-to-date lists by J. L. Moxham and A. Flammenkamp. It is believed that all multiperfect numbers of index 3, 4, 5, 6, and 7 are known. The number of known 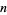 -multiperfect numbers are 1, 37, 6, 36, 65, 245, 516, 1134, 2036, 644, 1, 0, ... (Moxham 2001, Flammenkamp, Woltman 2000). Moxham (2000) found the largest known multiperfect number, approximately equal to
-multiperfect numbers are 1, 37, 6, 36, 65, 245, 516, 1134, 2036, 644, 1, 0, ... (Moxham 2001, Flammenkamp, Woltman 2000). Moxham (2000) found the largest known multiperfect number, approximately equal to 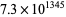 , on Feb. 13, 2000.
, on Feb. 13, 2000.
If 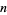 is a
is a 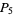 number such that
number such that 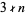 , then
, then 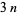 is a
is a 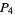 number. If
number. If 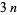 is a
is a 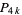 number such that
number such that 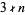 , then
, then 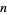 is a
is a 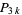 number. If
number. If 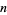 is a
is a 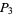 number such that 3 (but not 5 and 9) divides
number such that 3 (but not 5 and 9) divides 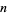 , then
, then 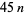 is a
is a 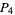 number.
number.
REFERENCES:
Beck, W. and Najar, R. "A Lower Bound for Odd Triperfects." Math. Comput. 38, 249-251, 1982.
Brown, A. L. "Multiperfect Numbers." Scripta Math. 20, 103-106, 1954.
Carmichael and Mason, T. E. Proc. Indian Acad. Sci., 257-270, 1911.
Cohen, G. L. and Hagis, P. Jr. "Results Concerning Odd Multiperfect Numbers." Bull. Malaysian Math. Soc. 8, 23-26, 1985.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 33-38, 2005.
Flammenkamp, A. "Multiply Perfect Numbers." https://www.uni-bielefeld.de/~achim/mpn.html.
Franqui, B. and García, M. "Some New Multiply Perfect Numbers." Amer. Math. Monthly 60, 459-462, 1953.
Franqui, B. and García, M. "57 New Multiply Perfect Numbers." Scripta Math. 20, 169-171, 1954.
Guy, R. K. "Almost Perfect, Quasi-Perfect, Pseudoperfect, Harmonic, Weird, Multiperfect and Hyperperfect Numbers." §B2 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 45-53, 1994.
Helenius, F. W. "Multiperfect Numbers (MPFNs)." https://home.netcom.com/~fredh/mpfn/.
Lehmer, D. N. Ann. Math. 2, 103-104, 1900-1901.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 149-151, 1979.
Moxham, J. L. "New Largest MPFN." mpfn@cs.arizona.edu posting, 13 Feb 2000.
Moxham, J. L. "1 New mpfns Total=4683." mpfn@cs.arizona.edu posting, 26 Mar 2001.
Perrier, J.-Y. "The Multi-Perfect Numbers." https://diwww.epfl.ch/~perrier/Multiparfaits.html
Poulet, P. La Chasse aux nombres, Vol. 1. Brussels, pp. 9-27, 1929.
Schroeppel, R. "Multiperfect Numbers-Multiply Perfect Numbers-Pluperfect Numbers-MPFNs." Rev. Dec. 13, 1995. ftp://ftp.cs.arizona.edu/xkernel/rcs/mpfn.html.
Schroeppel, R. (moderator). mpfn mailing list. e-mail rcs@cs.arizona.edu to subscribe.
Sloane, N. J. A. Sequences A000396/M4186, A005820/M5376, A027687, A046060, and A046061 in "The On-Line Encyclopedia of Integer Sequences."
Sorli, R. "Multiperfect Numbers." https://www-staff.maths.uts.edu.au/~rons/mpfn/mpfn.htm.
Woltman, G. "5 new MPFNs." mpfn@cs.arizona.edu posting, 23 Sep 2000.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|