


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-1-2021
Date: 30-1-2021
Date: 20-9-2020
|
An amicable pair 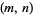 consists of two integers
consists of two integers 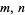 for which the sum of proper divisors (the divisors excluding the number itself) of one number equals the other. Amicable pairs are occasionally called friendly pairs (Hoffman 1998, p. 45), although this nomenclature is to be discouraged since the numbers more commonly known as friendly pairs are defined by a different, albeit related, criterion. Symbolically, amicable pairs satisfy
for which the sum of proper divisors (the divisors excluding the number itself) of one number equals the other. Amicable pairs are occasionally called friendly pairs (Hoffman 1998, p. 45), although this nomenclature is to be discouraged since the numbers more commonly known as friendly pairs are defined by a different, albeit related, criterion. Symbolically, amicable pairs satisfy
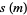 |
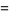 |
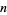 |
(1) |
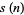 |
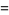 |
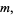 |
(2) |
where
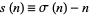 |
(3) |
is the restricted divisor function. Equivalently, an amicable pair 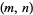 satisfies
satisfies
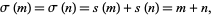 |
(4) |
where 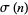 is the divisor function. The smallest amicable pair is (220, 284) which has factorizations
is the divisor function. The smallest amicable pair is (220, 284) which has factorizations
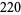 |
 |
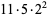 |
(5) |
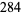 |
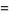 |
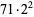 |
(6) |
giving restricted divisor functions
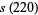 |
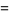 |
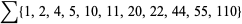 |
(7) |
 |
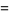 |
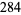 |
(8) |
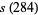 |
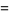 |
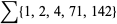 |
(9) |
 |
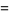 |
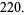 |
(10) |
The quantity
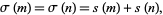 |
(11) |
in this case, 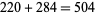 , is called the pair sum. The first few amicable pairs are (220, 284), (1184, 1210), (2620, 2924) (5020, 5564), (6232, 6368), (10744, 10856), (12285, 14595), (17296, 18416), (63020, 76084), ... (OEIS A002025 and A002046). An exhaustive tabulation is maintained by D. Moews.
, is called the pair sum. The first few amicable pairs are (220, 284), (1184, 1210), (2620, 2924) (5020, 5564), (6232, 6368), (10744, 10856), (12285, 14595), (17296, 18416), (63020, 76084), ... (OEIS A002025 and A002046). An exhaustive tabulation is maintained by D. Moews.
In 1636, Fermat found the pair (17296, 18416) and in 1638, Descartes found (9363584, 9437056), although these results were actually rediscoveries of numbers known to Arab mathematicians. By 1747, Euler had found 30 pairs, a number which he later extended to 60. In 1866, 16-year old B. Nicolò I. Paganini found the small amicable pair (1184, 1210) which had eluded his more illustrious predecessors (Paganini 1866-1867; Dickson 2005, p. 47). There were 390 known amicable pairs as of 1946 (Escott 1946). There are a total of 236 amicable pairs below 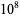 (Cohen 1970), 1427 below
(Cohen 1970), 1427 below 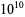 (te Riele 1986), 3340 less than
(te Riele 1986), 3340 less than 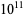 (Moews and Moews 1993ab), 4316 less than
(Moews and Moews 1993ab), 4316 less than 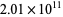 (Moews and Moews 1996), and 5001 less than
(Moews and Moews 1996), and 5001 less than 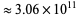 (Moews and Moews 1996).
(Moews and Moews 1996).
Rules for producing amicable pairs include the Thâbit ibn Kurrah rule rediscovered by Fermat and Descartes and extended by Euler to Euler's rule. A further extension not previously noticed was discovered by Borho (1972).
Pomerance (1981) has proved that
![[amicable numbers <=n]<ne^(-[ln(n)]^(1/3))](https://mathworld.wolfram.com/images/equations/AmicablePair/NumberedEquation4.gif) |
(12) |
for large enough 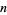 (Guy 1994). No nonfinite lower bound has been proven.
(Guy 1994). No nonfinite lower bound has been proven.
Let an amicable pair be denoted 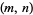 , and take
, and take 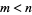 .
. 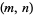 is called a regular amicable pair of type
is called a regular amicable pair of type 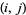 if
if
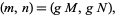 |
(13) |
where 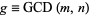 is the greatest common divisor,
is the greatest common divisor,
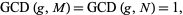 |
(14) |
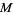 and
and 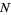 are squarefree, then the number of prime factors of
are squarefree, then the number of prime factors of 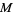 and
and 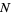 are
are 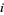 and
and 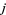 . Pairs which are not regular are called irregular or exotic (te Riele 1986). There are no regular pairs of type
. Pairs which are not regular are called irregular or exotic (te Riele 1986). There are no regular pairs of type 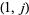 for
for 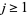 . If
. If 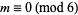 and
and
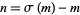 |
(15) |
is even, then 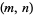 cannot be an amicable pair (Lee 1969). The minimal and maximal values of
cannot be an amicable pair (Lee 1969). The minimal and maximal values of 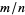 found by te Riele (1986) were
found by te Riele (1986) were
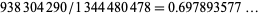 |
(16) |
and
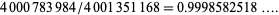 |
(17) |
te Riele (1986) also found 37 pairs of amicable pairs having the same pair sum. The first such pair is (609928, 686072) and (643336, 652664), which has the pair sum
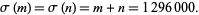 |
(18) |
te Riele (1986) found no amicable 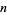 -tuples having the same pair sum for
-tuples having the same pair sum for 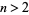 . However, Moews and Moews found a triple in 1993, and te Riele found a quadruple in 1995. In November 1997, a quintuple and sextuple were discovered. The sextuple is (1953433861918, 2216492794082), (1968039941816, 2201886714184), (1981957651366, 2187969004634), (1993501042130, 2176425613870), (2046897812505, 2123028843495), (2068113162038, 2101813493962), all having pair sum 4169926656000. Amazingly, the sextuple is smaller than any known quadruple or quintuple, and is likely smaller than any quintuple.
. However, Moews and Moews found a triple in 1993, and te Riele found a quadruple in 1995. In November 1997, a quintuple and sextuple were discovered. The sextuple is (1953433861918, 2216492794082), (1968039941816, 2201886714184), (1981957651366, 2187969004634), (1993501042130, 2176425613870), (2046897812505, 2123028843495), (2068113162038, 2101813493962), all having pair sum 4169926656000. Amazingly, the sextuple is smaller than any known quadruple or quintuple, and is likely smaller than any quintuple.
The earliest known odd amicable numbers all were divisible by 3. This led Bratley and McKay (1968) to conjecture that there are no amicable pairs coprime to 6 (Guy 1994, p. 56). However, Battiato and Borho (1988) found a counterexample, and now many amicable pairs are known which are not divisible by 6 (Pedersen). The smallest known example of this kind is the amicable pair (42262694537514864075544955198125, 42405817271188606697466971841875), each number of which has 32 digits.
A search was then begun for amicable pairs coprime to 30. The first example was found by Y. Kohmoto in 1997, consisting of a pair of numbers each having 193 digits (Pedersen). Kohmoto subsequently found two other examples, and te Riele and Pedersen used two of Kohmoto's examples to calculated 243 type-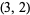 pairs coprime to 30 by means of a method which generates type-
pairs coprime to 30 by means of a method which generates type-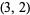 pairs from a type-
pairs from a type-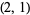 pairs.
pairs.
No amicable pairs which are coprime to 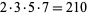 are currently known.
are currently known.
The following table summarizes the largest known amicable pairs discovered in recent years. The largest of these is obtained by defining
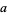 |
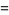 |
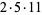 |
(19) |
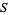 |
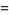 |
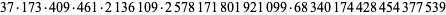 |
(20) |
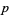 |
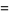 |
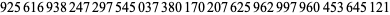 |
(21) |
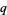 |
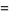 |
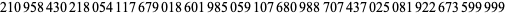 |
(22) |
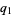 |
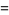 |
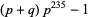 |
(23) |
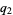 |
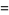 |
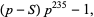 |
(24) |
then 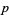 ,
, 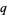 ,
, 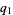 and
and 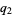 are all primes, and the numbers
are all primes, and the numbers
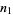 |
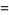 |
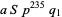 |
(25) |
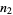 |
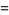 |
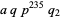 |
(26) |
are an amicable pair, with each member having 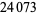 decimal digits (Jobling 2005).
decimal digits (Jobling 2005).
| digits | date | reference |
| 4829 | Oct. 4, 1997 | M. García |
| 8684 | Jun. 6, 2003 | Jobling and Walker 2003 |
| 16563 | May 12, 2004 | Walker et al. 2004 |
| 17326 | May 12, 2004 | Walker et al. 2004 |
| 24073 | Mar. 10, 2005 | Jobling 2005 |
Amicable pairs in Gaussian integers also exist, for example
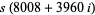 |
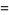 |
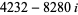 |
(27) |
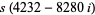 |
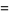 |
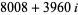 |
(28) |
and
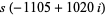 |
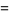 |
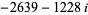 |
(29) |
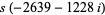 |
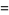 |
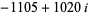 |
(30) |
(T. D. Noe, pers. comm.).
REFERENCES:
Alanen, J.; Ore, Ø.; and Stemple, J. "Systematic Computations on Amicable Numbers." Math. Comput. 21, 242-245, 1967.
Battiato, S. and Borho, W. "Are there Odd Amicable Numbers not Divisible by Three?" Math. Comput. 50, 633-637, 1988.
Borho, W. "On Thabit ibn Kurrah's Formula for Amicable Numbers." Math. Comput. 26, 571-578, 1972.
Borho, W. "Some Large Primes and Amicable Numbers." Math. Comput. 36, 303-304, 1981.
Borho, W. "Befreundete Zahlen: Ein zweitausend Jahre altes Thema der elementaren Zahlentheorie." In Mathematische Miniaturen 1: Lebendige Zahlen: Fünf Exkursionen. Basel, Switzerland: Birkhäuser, pp. 5-38, 1981.
Borho, W. and Hoffmann, H. "Breeding Amicable Numbers in Abundance." Math. Comput. 46, 281-293, 1986.
Bratley, P.; Lunnon, F.; and McKay, J. "Amicable Numbers and Their Distribution." Math. Comput. 24, 431-432, 1970.
Bratley, P. and McKay, J. "More Amicable Numbers." Math. Comput. 22, 677-678, 1968.
Cohen, H. "On Amicable and Sociable Numbers." Math. Comput. 24, 423-429, 1970.
Costello, P. "Amicable Pairs of Euler's First Form." J. Rec. Math. 10, 183-189, 1977-1978.
Costello, P. "Amicable Pairs of the Form 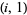 ." Math. Comput. 56, 859-865, 1991.
." Math. Comput. 56, 859-865, 1991.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 38-50, 2005.
Dubner, H. "New Amicable Pair Record." Oct. 14, 1997. https://listserv.nodak.edu/scripts/wa.exe?A2=ind9710&L=NMBRTHRY&F=&S=&P=695.
Erdős, P. "On Amicable Numbers." Publ. Math. Debrecen 4, 108-111, 1955-1956.
Erdős, P. "On Asymptotic Properties of Aliquot Sequences." Math. Comput. 30, 641-645, 1976.
Escott, E. B. E. "Amicable Numbers." Scripta Math. 12, 61-72, 1946.
García, M. "New Amicable Pairs." Scripta Math. 23, 167-171, 1957.
Gardner, M. "Perfect, Amicable, Sociable." Ch. 12 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 160-171, 1978.
Guy, R. K. "Amicable Numbers." §B4 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 55-59, 1994.
Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, 1998.
Jobling, P. "Large Amicable Pairs." Jun. 6, 2004. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0306&L=nmbrthry&P=R97&D=0.
Jobling, P. "A New Largest Known Amicable Pair." Mar. 10, 2005. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0503&L=nmbrthry&F=&S=&P=552.
Lee, E. J. "Amicable Numbers and the Bilinear Diophantine Equation." Math. Comput. 22, 181-197, 1968.
Lee, E. J. "On Divisibility of the Sums of Even Amicable Pairs." Math. Comput. 23, 545-548, 1969.
Lee, E. J. and Madachy, J. S. "The History and Discovery of Amicable Numbers, I." J. Rec. Math. 5, 77-93, 1972.
Lee, E. J. and Madachy, J. S. "The History and Discovery of Amicable Numbers, II." J. Rec. Math. 5, 153-173, 1972.
Lee, E. J. and Madachy, J. S. "The History and Discovery of Amicable Numbers, III." J. Rec. Math. 5, 231-249, 1972.
Lee, E. J. and Madachy, J. S. Errata to "The History and Discovery of Amicable Numbers, I-III." J. Rec. Math. 6, 53, 164, and 229, 1973.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 145 and 155-156, 1979.
Moews, D. and Moews, P. C. "A Search for Aliquot Cycles and Amicable Pairs." Math. Comput. 61, 935-938, 1993a.
Moews, D. and Moews, P. C. "A List of Amicable Pairs Below 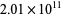 ." Rev. Jan. 8, 1993b. https://xraysgi.ims.uconn.edu:8080/amicable.txt.
." Rev. Jan. 8, 1993b. https://xraysgi.ims.uconn.edu:8080/amicable.txt.
Moews, D. and Moews, P. C. "A List of the First 5001 Amicable Pairs." Rev. Jan. 7, 1996. https://xraysgi.ims.uconn.edu:8080/amicable2.txt.
Ore, Ø. Number Theory and Its History. New York: Dover, pp. 96-100, 1988.
Paganini, B. N. I. Atti della R. Accad. Sc. Torino 2, 362, 1866-1867.
Pedersen, J. M. "Known Amicable Pairs." https://amicable.homepage.dk/knwnc2.htm
Pedersen, J. M. "Various Amicable Pair Lists and Statistics." https://amicable.homepage.dk/apstat.htm
Pomerance, C. "On the Distribution of Amicable Numbers." J. reine angew. Math. 293/294, 217-222, 1977.
Pomerance, C. "On the Distribution of Amicable Numbers, II." J. reine angew. Math. 325, 182-188, 1981.
Root, S. Item 61 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 23, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item61.
Sloane, N. J. A. Sequences A002025/M5414 and A002046/M5435 in "The On-Line Encyclopedia of Integer Sequences."
Souissi, M. Un Texte Manuscrit d'Ibn Al-Bannā' Al-Marrakusi sur les Nombres Parfaits, Abondants, Deficients, et Amiables. Karachi, Pakistan: Hamdard Nat. Found., 1975.
Speciner, M. Item 62 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 24, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item62.
te Riele, H. J. J. "Four Large Amicable Pairs." Math. Comput. 28, 309-312, 1974.
te Riele, H. J. J. "On Generating New Amicable Pairs from Given Amicable Pairs." Math. Comput. 42, 219-223, 1984.
te Riele, H. J. J. "Computation of All the Amicable Pairs Below 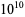 ." Math. Comput. 47, 361-368 and S9-S35, 1986.
." Math. Comput. 47, 361-368 and S9-S35, 1986.
te Riele, H. J. J.; Borho, W.; Battiato, S.; Hoffmann, H.; and Lee, E. J. "Table of Amicable Pairs Between 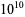 and
and 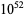 ." Centrum voor Wiskunde en Informatica, Note NM-N8603. Amsterdam: Stichting Math. Centrum, 1986.
." Centrum voor Wiskunde en Informatica, Note NM-N8603. Amsterdam: Stichting Math. Centrum, 1986.
te Riele, H. J. J. "A New Method for Finding Amicable Pairs." In Mathematics of Computation 1943-1993: A Half-Century of Computational Mathematics (Vancouver, BC, August 9-13, 1993) (Ed. W. Gautschi). Providence, RI: Amer. Math. Soc., pp. 577-581, 1994.
Walker, A. "New Large Amicable Pairs." May 12, 2004. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0405&L=nmbrthry&F=&S=&P=1043.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|