If  is prime, then 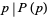, where  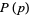is a member of the Perrin sequence 3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, ... (OEIS A001608). A Perrin pseudoprime is a composite number  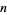such that 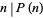. Several "unrestricted" Perrin pseudoprimes are known, the smallest of which are 271441, 904631, 16532714, 24658561, ... (OEIS A013998).

Adams and Shanks (1982) discovered the smallest unrestricted Perrin pseudoprime after unsuccessful searches by Perrin (1899), Malo (1900), Escot (1901), and Jarden (1966). (A 1996 article by Stewart's stating that no Perrin pseudoprimes were then known was incorrect.)

Grantham generalized the definition of Perrin pseudoprime with parameters 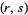 to be an odd composite number  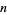for which either

1. 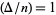 and 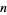 has an S-recurrence relation signature, or

2. 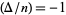 and 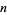 has a Q-recurrence relation signature,

where 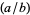 is the Jacobi symbol. All the 55 Perrin pseudoprimes less than  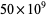have been computed by Kurtz et al. (1986). All have S-recurrence relation signature, and form the sequence Sloane calls "restricted" Perrin pseudoprimes: 27664033, 46672291, 102690901, ... (OEIS A018187).

REFERENCES:

Adams, W. W. "Characterizing Pseudoprimes for Third-Order Linear Recurrence Sequences." Math Comput. 48, 1-15, 1987.

Adams, W. and Shanks, D. "Strong Primality Tests that Are Not Sufficient." Math. Comput. 39, 255-300, 1982.

Bach, E. and Shallit, J. Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA: MIT Press, p. 305, 1996.

Escot, E.-B. "Solution to Item 1484." L'Intermédiare des Math. 8, 63-64, 1901.

Grantham, J. "Frobenius Pseudoprimes." http://www.clark.net/pub/grantham/pseudo/pseudo1.ps.

Holzbaur, C. "Perrin Pseudoprimes." http://ftp.ai.univie.ac.at/perrin.html.

Jarden, D. Recurring Sequences: A Collection of Papers, Including New Factorizations of Fibonacci and Lucas Numbers. Jerusalem: Riveon Lematematika, 1966.

Kurtz, G. C.; Shanks, D.; and Williams, H. C. "Fast Primality Tests for Numbers Less than 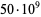." Math. Comput. 46, 691-701, 1986.

Malo, E. L'Intermédiare des Math. 7, 281 and 312, 1900.

Perrin, R. "Item 1484." L'Intermédiare des Math. 6, 76-77, 1899.

Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, p. 135, 1996.

Sloane, N. J. A. Sequences A001608/M0429, A013998, and A018187 in "The On-Line Encyclopedia of Integer Sequences."

Stewart, I. "Tales of a Neglected Number." Sci. Amer. 274, 102-103, June 1996.

اخر الاخبار

اخبار العتبة العباسية المقدسة

مجموعة مشاتل الكفيل: إضافة نحو 70 نوعًا جديدًا من المغروسات تتناسب مع الظروف المناخية المحلية

المجمَع العلمي يطلق الدورة التطويرية الخامسة لمعلمي التربية الإسلامية ومدرسيها في النجف الأشرف

خدمات إنسانية متنوّعة تقدّمها شعبة الشهداء والجرحى في مختلف المحافظات

قسم العلاقات العامة يطلق فعاليات مخيم البذرة الواعدة الخاص بأبناء المنتسبين

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد