


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-11-2020
Date: 16-5-2020
Date: 11-11-2019
|
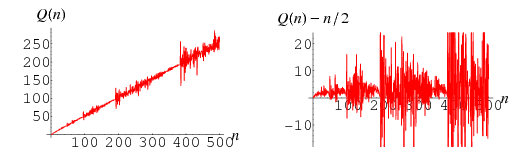
The recursive sequence generated by the recurrence equation
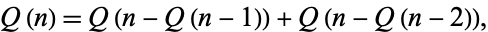 |
with 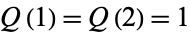 . The first few values are 1, 1, 2, 3, 3, 4, 5, 5, 6, 6, ... (OEIS A005185; Wolfram 2002, pp. 129-130, sequence (e)). These numbers are sometimes called
. The first few values are 1, 1, 2, 3, 3, 4, 5, 5, 6, 6, ... (OEIS A005185; Wolfram 2002, pp. 129-130, sequence (e)). These numbers are sometimes called 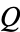 -numbers. The Hofstadter
-numbers. The Hofstadter 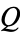 -sequence can be implemented in the Wolfram Language as
-sequence can be implemented in the Wolfram Language as
Hofstadter[1] = Hofstadter[2] = 1;
Hofstadter[n_Integer?Positive] := Hofstadter[n] = Block[
{$RecursionLimit = Infinity},
Hofstadter[n - Hofstadter[n - 1]] +
Hofstadter[n - Hofstadter[n - 2]]
]
There are currently no rigorous analyses or detailed predictions of the rather erratic behavior of 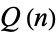 (Guy 1994). It has, however, been demonstrated that the chaotic behavior of the
(Guy 1994). It has, however, been demonstrated that the chaotic behavior of the 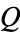 -numbers shows some signs of order, namely that they exhibit approximate period doubling, self-similarity and scaling (Pinn 1999, 2000). These properties are shared with the related sequence
-numbers shows some signs of order, namely that they exhibit approximate period doubling, self-similarity and scaling (Pinn 1999, 2000). These properties are shared with the related sequence
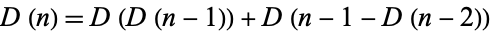 |
with 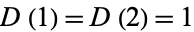 , which exhibits exact period doubling (Pinn 1999, 2000). The chaotic regions of
, which exhibits exact period doubling (Pinn 1999, 2000). The chaotic regions of 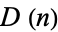 are separated by predictable smooth behavior.
are separated by predictable smooth behavior.
REFERENCES:
Conolly, B. W. "Fibonacci and Meta-Fibonacci Sequences." In Fibonacci and Lucas Numbers, and the Golden Section (Ed. S. Vajda). New York: Halstead Press, pp. 127-138, 1989.
Dawson, R.; Gabor, G.; Nowakowski, R.; and Weins, D. "Random Fibonacci-Type Sequences." Fib. Quart. 23, 169-176, 1985.
Guy, R. "Some Suspiciously Simple Sequences." Amer. Math. Monthly 93, 186-191, 1986.
Guy, R. K. "Three Sequences of Hofstadter." §E31 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 231-232, 1994.
Hofstadter, D. R. Gödel, Escher Bach: An Eternal Golden Braid. New York: Vintage Books, pp. 137-138, 1980.
Kubo, T. and Vakil, R. "On Conway's Recursive Sequence." Disc. Math. 152, 225-252, 1996.
Mallows, C. L. "Conway's Challenge Sequence." Amer. Math. Monthly 98, 5-20, 1991.
Pickover, C. A. "The Crying of Fractal Batrachion 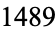 ." Comput. & Graphics 19, 611-615, 1995. Reprinted in Chaos and Fractals, A Computer Graphical Journey: Ten Year Compilation of Advanced Research (Ed. C. A. Pickover). Amsterdam, Netherlands: Elsevier, pp. 127-131, 1998.
." Comput. & Graphics 19, 611-615, 1995. Reprinted in Chaos and Fractals, A Computer Graphical Journey: Ten Year Compilation of Advanced Research (Ed. C. A. Pickover). Amsterdam, Netherlands: Elsevier, pp. 127-131, 1998.
Pickover, C. A. "The Crying of Fractal Batrachion 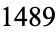 ." Ch. 25 in Keys to Infinity. New York: W. H. Freeman, pp. 183-191, 1995.
." Ch. 25 in Keys to Infinity. New York: W. H. Freeman, pp. 183-191, 1995.
Pinn, K. "Order and Chaos is Hofstadter's 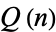 Sequence." Complexity 4, 41-46, 1999.
Sequence." Complexity 4, 41-46, 1999.
Pinn, K. "A Chaotic Cousin of Conway's Recursive Sequence." Exper. Math. 9, 55-66, 2000.
Sloane, N. J. A. Sequence A005185/M0438 in "The On-Line Encyclopedia of Integer Sequences."
Tanny, S. M. "A Well-Behaved Cousin of the Hofstadter Sequence." Disc. Math. 105, 227-239, 1992.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 129-130, 2002.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|