


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-11-2020
Date: 12-9-2020
Date: 17-12-2019
|
Form a sequence from an alphabet of letters ![[1,n]](https://mathworld.wolfram.com/images/equations/Davenport-SchinzelSequence/Inline1.gif) such that there are no consecutive letters and no alternating subsequences of length greater than
such that there are no consecutive letters and no alternating subsequences of length greater than 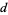 . Then the sequence is a Davenport-Schinzel sequence if it has maximal length
. Then the sequence is a Davenport-Schinzel sequence if it has maximal length 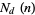 . The value of
. The value of 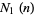 is the trivial sequence of 1s: 1, 1, 1, ... (OEIS A000012). The values of
is the trivial sequence of 1s: 1, 1, 1, ... (OEIS A000012). The values of 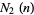 are the positive integers 1, 2, 3, 4, ... (OEIS A000027). The values of
are the positive integers 1, 2, 3, 4, ... (OEIS A000027). The values of 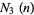 are the odd integers 1, 3, 5, 7, ... (OEIS A005408). The first nontrivial Davenport-Schinzel sequence
are the odd integers 1, 3, 5, 7, ... (OEIS A005408). The first nontrivial Davenport-Schinzel sequence 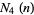 is given by 1, 4, 8, 12, 17, 22, 27, 32, ... (OEIS A002004). Additional sequences are given by Guy (1994, p. 221) and Sloane.
is given by 1, 4, 8, 12, 17, 22, 27, 32, ... (OEIS A002004). Additional sequences are given by Guy (1994, p. 221) and Sloane.
REFERENCES:
Agarwal, P. K. and Sharir, M. "Davenport-Schinzel Sequences and Their Geometric Applications." Ch. 1 in Handbook of Computational Geometry (Ed. J.-R. Sack and J. Urrutia). Amsterdam, Netherlands: North-Holland, pp. 1-47, 2000.
Davenport, H. and Schinzel, A. "A Combinatorial Problem Connected with Differential Equations." Amer. J. Math. 87, 684-690, 1965.
Guy, R. K. "Davenport-Schinzel Sequences." §E20 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 220-222, 1994.
Roselle, D. P. and Stanton, R. G. "Results of Davenport-Schinzel Sequences." In Proc. Louisiana Conference on Combinatorics, Graph Theory, and Computing. Louisiana State University, Baton Rouge, March 1-5, 1970 (Ed. R. C. Mullin, K. B. Reid, and D. P. Roselle). Winnipeg, Manitoba: Utilitas Mathematica, pp. 249-267, 1960.
Sharir, M. and Agarwal, P. Davenport-Schinzel Sequences and Their Geometric Applications. New York: Cambridge University Press, 1995.
Sloane, N. J. A. Sequences A000012/M0003, A000027/M0472, and A002004/M3328 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|