


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-1-2021
Date: 22-12-2019
Date: 8-9-2020
|
Any nonzero rational number  can be represented by
can be represented by
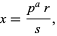 |
(1) |
where 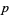 is a prime number,
is a prime number, 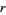 and
and 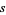 are integers not divisible by
are integers not divisible by 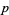 , and
, and 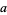 is a unique integer. The p-adic norm of
is a unique integer. The p-adic norm of  is then defined by
is then defined by
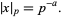 |
(2) |
Also define the 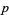 -adic value
-adic value
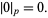 |
(3) |
As an example, consider the fraction
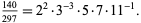 |
(4) |
It has 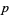 -adic absolute values given by
-adic absolute values given by
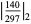 |
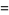 |
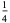 |
(5) |
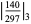 |
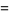 |
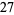 |
(6) |
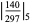 |
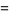 |
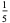 |
(7) |
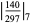 |
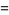 |
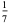 |
(8) |
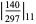 |
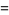 |
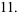 |
(9) |
The 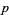 -adic norm of a nonzero rational number
-adic norm of a nonzero rational number  can be computed in the Wolfram Language as follows.
can be computed in the Wolfram Language as follows.
PadicNorm[x_Integer, p_Integer?PrimeQ] :=
p^(-IntegerExponent[x, p])
PadicNorm[x_Rational, p_Integer?PrimeQ] :=
PadicNorm[Numerator[x], p] /
PadicNorm[Denominator[x], p]
The 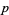 -adic norm satisfies the relations
-adic norm satisfies the relations
1. 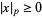 for all
for all  ,
,
2. 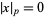 iff
iff 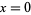 ,
,
3. 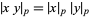 for all
for all  and
and 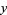 ,
,
4. 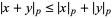 for all
for all  and
and 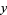 (the triangle inequality), and
(the triangle inequality), and
5. 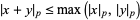 for all
for all  and
and 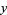 (the strong triangle inequality).
(the strong triangle inequality).
In the above, relation 4 follows trivially from relation 5, but relations 4 and 5 are relevant in the more general valuation theory.
The p-adic norm is the basis for the algebra of p-adic numbers.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|