المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Barban,s Constant |
 535
 10:25 صباحاً
date: 1-10-2020 |
Author : Barban, M. B 
Book or Source : "The Large Sieve Method and Its Application to Number Theory." Uspehi Mat. Nauk 21 
Page and Part : ...|
Read More
Date: 11-2-2020
2566
Date: 24-8-2020
2024
Date: 28-10-2019
1051
|
Barban's constant is defined as
 |
 |
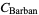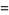![product_(p)[1+(3p^2-1)/(p(p+1)(p^2-1))]](https://mathworld.wolfram.com/images/equations/BarbansConstant/Inline3.gif) |
(1) |
 |
 |
 |
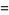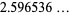(2) |
(OEIS A175640), where the product is over the primes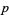 
.
REFERENCES:
Barban, M. B. "The Large Sieve Method and Its Application to Number Theory." Uspehi Mat. Nauk 21, 51-102, 1966.
Finch, S. "Class Number Theory." https://algo.inria.fr/csolve/clss.pdf. May 6, 2005.
Sloane, N. J. A. Sequence A175640 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
