Woodall Prime

A Woodall prime is a Woodall number

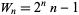that is prime. The first few Woodall primes are 7, 23, 383, 32212254719, 2833419889721787128217599, ... (OEIS A050918), corresponding to 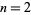, 3, 6, 30, 75, 81, 115, 123, 249, 362, 384, 462, 512, 751, 822, 5312, 7755, 9531, 12379, ... (OEIS A002234).

The following table summarizes large known Woodall primes. As of Mar. 2018, all 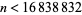 have been checked (PrimeGrid).

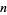	decimal digits	date
1467763	441847	Jun. 2007
2013992	606279	Aug. 2007
2367906	712818	Aug. 2007
3752948	1129757	Dec. 2007
17016602	5122515	Mar. 2018

REFERENCES:

Caldwell, C. K. "The Top Twenty: Woodall Primes." https://primes.utm.edu/top20/page.php?id=7#records.

Keller, W. "New Cullen Primes." Math. Comput. 64, 1733-1741, 1995.

Leyland, P. https://research.microsoft.com/~pleyland/factorization/cullen_woodall/2-.txt.

PrimeGrid. "Subprojects: Woodall Prime Search." https://www.primegrid.com/server_status_subprojects.php.

PrimeGrid. "PrimeGrid Primes: Subproject: (WOO) Woodall Prime Search." https://www.primegrid.com/primes/primes.php?project=WOO.

Rodenkirch, M. and Ballinger, R. "Woodall Primes: Definition and Status." https://www.prothsearch.net/woodall.html.

Sloane, N. J. A. Sequences A002234/M0820 and A050918 in "The On-Line Encyclopedia of Integer Sequences."