Perrin Sequence

The integer sequence defined by the recurrence

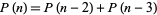(1)

with the initial conditions 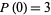, , 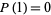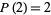. This recurrence relation is the same as that for the Padovan sequence but with different initial conditions. The first few terms for 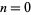, 1, ..., are 3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, ... (OEIS A001608).

The above cartoon (Amend 2005) shows an unconventional sports application of the Perrin sequence (right panel). (The left two panels instead apply the Fibonacci numbers).

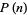 is the solution of a third-order linear homogeneous recurrence equation having characteristic equation

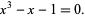(2)

Denoting the roots of this equation by 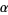, , 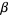and 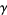, with  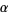the unique real root, the solution is then

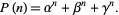(3)

Here,

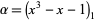(4)

is the plastic constant 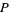, which is also given by the limit

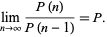(5)

The asymptotic behavior of 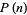 is

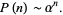(6)

The first few primes in this sequence are 2, 3, 2, 5, 5, 7, 17, 29, 277, 367, 853, ... (OEIS A074788), which occur for terms 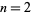, 3, 4, 5, 6, 7, 10, 12, 20, 21, 24, 34, 38, 75, 122, 166, 236, 355, 356, 930, 1042, 1214, 1461, 1622, 4430, 5802, 9092, 16260, 18926, 23698, 40059, 45003, 73807, 91405, 263226, 316872, 321874, 324098, ... (OEIS A112881), the largest of which are probable primes and a number of which are summarized in the following table.

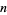	decimal digits	discoverer	date
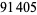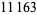		E. W. Weisstein	Oct. 6, 2005
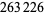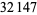		E. W. Weisstein	May 4, 2006
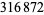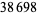		E. W. Weisstein	Feb. 4, 2007
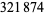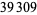		E. W. Weisstein	Feb. 19, 2007
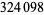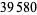		E. W. Weisstein	Feb. 25, 2007
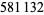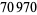		E. W. Weisstein	Feb. 15, 2011

Perrin (1899) investigated the sequence and noticed that if 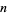 is prime, then  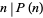(i.e.,  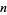divides 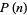). The first statement of this fact is attributed to É. Lucas in 1876 by Stewart (1996). Perrin also searched for but did not find any composite number  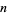in the sequence such that 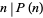. Such numbers are now known as Perrin pseudoprimes. Malo (1900), Escot (1901), and Jarden (1966) subsequently investigated the series and also found no Perrin pseudoprimes. Adams and Shanks (1982) subsequently found that  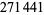is such a number.

REFERENCES:

Adams, W. and Shanks, D. "Strong Primality Tests that Are Not Sufficient." Math. Comput. 39, 255-300, 1982.

Amend, B. "FoxTrot.com." Cartoon from Oct. 11, 2005. https://www.foxtrot.com/.

Escot, E.-B. "Solution to Item 1484." L'Intermédiare des Math. 8, 63-64, 1901.

Jarden, D. Recurring Sequences: A Collection of Papers, Including New Factorizations of Fibonacci and Lucas Numbers. Jerusalem: Riveon Lematematika, 1966.

Malo, E. L'Intermédiare des Math. 7, 281 and 312, 1900.

Perrin, R. "Item 1484." L'Intermédiare des Math. 6, 76-77, 1899.

Sloane, N. J. A. Sequences A001608/M0429, A074788, and A112881 in "The On-Line Encyclopedia of Integer Sequences."

Stewart, I. "Tales of a Neglected Number." Sci. Amer. 274, 102-103, June 1996.a