RSA Number

RSA numbers are difficult to-factor composite numbers having exactly two prime factors (i.e., so-called semiprimes) that were listed in the Factoring Challenge of RSA Security®--a challenge that is now withdrawn and no longer active.

While RSA numbers are much smaller than the largest known primes, their factorization is significant because of the curious property of numbers that proving or disproving a number to be prime ("primality testing") seems to be much easier than actually identifying the factors of a number ("prime factorization"). Thus, while it is trivial to multiply two large numbers 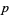 and 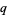 together, it can be extremely difficult to determine the factors if only their product  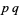is given. With some ingenuity, this property can be used to create practical and efficient encryption systems for electronic data.

RSA Laboratories sponsored the RSA Factoring Challenge to encourage research into computational number theory and the practical difficulty of factoring large integers, and because it can be helpful for users of the RSA encryption public-key cryptography algorithm for choosing suitable key lengths for an appropriate level of security.

RSA numbers were originally spaced at intervals of 10 decimal digits between 100 and 500 digits, and prizes were awarded according to a complicated formula. These original numbers were named according to the number of decimal digits, so RSA-100 was a hundred-digit number. As computers and algorithms became faster, the unfactored challenge numbers were removed from the prize list and replaced with a set of numbers with fixed cash prizes. At this point, the naming convention was also changed so that the trailing number would indicate the number of digits in the binary representation of the number. Hence, RSA-640 has 640 binary digits, which translates to 193 digits in decimal.

RSA numbers received widespread attention when a 129-digit number known as RSA-129 was used by R. Rivest, A. Shamir, and L. Adleman to publish one of the first public-key messages together with a $100 reward for the message's decryption (Gardner 1977). Despite widespread belief at the time that the message encoded by RSA-129 would take millions of years to break, it was factored in 1994 using a distributed computation which harnessed networked computers spread around the globe performing a multiple polynomial quadratic sieve (Leutwyler 1994). The result of all the concentrated number crunching was decryption of the encoded message to yield the profound plaintext message "The magic words are squeamish ossifrage." (For the benefit of non-ornithologists, an ossifrage is a rare predatory vulture found in the mountains of Europe.) The corresponding factorization (into a 64-digit number and a 65-digit number) is

(Leutwyler 1994, Cipra 1996).

RSA-129 is referred to in the Season 1 episode "Prime Suspect" of the television crime drama NUMB3RS.

On Feb. 2, 1999, a group led by H. te Riele completed factorization of RSA-140 into two 70-digit primes. In a preprint dated April 16, 2004, Aoki et al. factored RSA-150 into two 75-digit primes. On Aug. 22, 1999, a group led by H. te Riele completed factorization of RSA-155 into two 78-digit primes (te Riele 1999b, Peterson 1999). On December 2, Jens Franke circulated an email announcing factorization of the smallest prize number RSA-576 (Weisstein 2003). This factorization into two 87-digit factors was accomplished using a prime factorization algorithm known as the general number field sieve (GNFS). On May 9, 2005, the group led by Franke announced factorization of RSA-200 into two 100-digits primes (Weisstein 2005a), and in November 2005, the same group announced the factorization of RSA-674 (Weisstein 2005b).

On Jan. 7, 2010, Kleinjung announced factorization of the 768-bit, 232-digit number RSA-768 by the number field sieve, which is a record for factoring general integers. Both factors have 384 bits and 116 digits. Total sieving time was approximation 1500 AMD64 years (Kleinjung 2010, Kleinjung et al. 2010).

As the following table shows, while the Challenge has been withdrawn, most of the numbers RSA-704 to RSA-2048 have never been factored.

number	decimal digits	prize	factored (references)
RSA-100	100		Apr. 1991
RSA-110	110		Apr. 1992
RSA-120	120		Jun. 1993
RSA-129	129		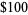Apr. 1994 (Leutwyler 1994, Cipra 1995)
RSA-130	130		Apr. 10, 1996
RSA-140	140		Feb. 2, 1999 (te Riele 1999a)
RSA-150	150		Apr. 6, 2004 (Aoki 2004)
RSA-155	155		Aug. 22, 1999 (te Riele 1999b, Peterson 1999)
RSA-160	160		Apr. 1, 2003 (Bahr et al. 2003)
RSA-200	200		May 9, 2005 (see Weisstein 2005a)
RSA-576	174		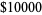Dec. 3, 2003 (Franke 2003; see Weisstein 2003)
RSA-640	193		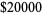Nov. 4, 2005 (see Weisstein 2005b)
RSA-704	212	withdrawn	Jul. 1, 2012 (Bai et al. 2012, Bai 2012)
RSA-768	232	withdrawn	Dec. 12, 2009 (Kleinjung 2010, Kleinjung et al. 2010)
RSA-896	270	withdrawn
RSA-1024	309	withdrawn
RSA-1536	463	withdrawn
RSA-2048	617	withdrawn

REFERENCES:

Aoki, K.; Kida, Y.; Shimoyama, T.; and Ueda, H. "GNFS Factoring Statistics of RSA-100, 110, ..., 150." April 16, 2004. https://eprint.iacr.org/2004/095.pdf.

Bahr, F.; Franke, J.; Kleinjung, T.; Lochter, M.; and Böhm, M. "RSA-160." https://www.loria.fr/~zimmerma/records/rsa160.

Bai, S.; Thomé, E.; and Zimmerman, P. "Factorisation of RSA-704 with CADO-NSF." https://maths.anu.edu.au/~bai/paper/rsa704.pdf. Jul. 1, 2012.

Bai, S. "Factorization of RSA704." 2 Jul 2012. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind1207&L=NMBRTHRY&F=&S=&P=923.

Cipra, B. "The Secret Life of Large Numbers." What's Happening in the Mathematical Sciences, 1995-1996, Vol. 3. Providence, RI: Amer. Math. Soc., pp. 90-99, 1996.

Cowie, J.; Dodson, B.; Elkenbracht-Huizing, R. M.; Lenstra, A. K.; Montgomery, P. L.; Zayer, J. A. "World Wide Number Field Sieve Factoring Record: On to 512 Bits." In Advances in Cryptology--ASIACRYPT '96 (Kyongju) (Ed. K. Kim and T. Matsumoto.) New York: Springer-Verlag, pp. 382-394, 1996.

Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, pp. 46-47, 2000.

Franke, J. "RSA576." Privately circulated email reposted to primenumbers Yahoo! Group. https://groups.yahoo.com/group/primenumbers/message/14113.

Gardner, M. "Mathematical Games: A New Kind of Cipher that Would Take Millions of Years to Break." Sci. Amer. 237, 120-124, Aug. 1977.

Klee, V. and Wagon, S. Old and New Unsolved Problems in Plane Geometry and Number Theory, rev. ed. Washington, DC: Math. Assoc. Amer., p. 223, 1991.

Kleinjung, T. et al. "Factorization of a 768-bit RSA Modulus." Version 1.0, Jan. 7, 2010. https://eprint.iacr.org/2010/006.pdf.

Kleinjung, T. "Factorization of a 768-bit RSA modulus." 7 Jan 2010. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind1001&L=nmbrthry&T=0&F=&S=&P=719.

Leutwyler, K. "Superhack: Forty Quadrillion Years Early, a 129-Digit Code is Broken." Sci. Amer. 271, 17-20, 1994.

Leyland, P. ftp://sable.ox.ac.uk/pub/math/rsa129

Peterson, I. "Crunching Internet Security Codes." Sci. News 156, 221, Oct. 2, 1999.

RSA Laboratories.® "The RSA Factoring Challenge" https://www.rsa.com/rsalabs/node.asp?id=2092.

Taubes, G. "Small Army of Code-breakers Conquers a 129-Digit Giant." Science 264, 776-777, 1994.

te Riele, H. "Factorisation of RSA-140." 4 Feb 1999a. https://listserv.nodak.edu/scripts/wa.exe?A2=ind9902&L=nmbrthry&P=302.

te Riele, H. "New Factorization Record." 26 Aug 1999b. https://listserv.nodak.edu/scripts/wa.exe?A2=ind9908&L=nmbrthry&P=1905.

Weisstein, E. "RSA-576 Factored." MathWorld Headline News, Dec. 5, 2003. https://mathworld.wolfram.com/news/2003-12-05/rsa/.

Weisstein, E. "RSA-200 Factored." MathWorld Headline News, May. 10, 2005a. https://mathworld.wolfram.com/news/2005-05-10/rsa-200/.

Weisstein, E. "RSA-640 Factored." MathWorld Headline News, Nov. 8, 2005b. https://mathworld.wolfram.com/news/2005-11-08/rsa-640/.