


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-10-2020
Date: 13-1-2021
Date: 29-12-2019
|
A Fermat prime is a Fermat number 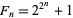 that is prime. Fermat primes are therefore near-square primes.
that is prime. Fermat primes are therefore near-square primes.
Fermat conjectured in 1650 that every Fermat number is prime and Eisenstein in 1844 proposed as a problem the proof that there are an infinite number of Fermat primes (Ribenboim 1996, p. 88). At present, however, the only Fermat numbers 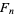 for
for 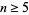 for which primality or compositeness has been established are all composite.
for which primality or compositeness has been established are all composite.
The only known Fermat primes are
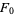 |
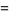 |
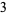 |
(1) |
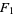 |
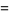 |
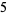 |
(2) |
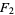 |
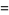 |
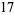 |
(3) |
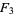 |
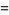 |
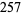 |
(4) |
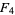 |
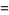 |
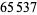 |
(5) |
(OEIS A019434), and it seems unlikely that any more will be found using current computational methods and hardware. It follows that 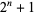 is prime for the special case
is prime for the special case 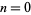 together with the Fermat prime indices, giving the sequence 2, 3, 5, 17, 257, and 65537 (OEIS A092506).
together with the Fermat prime indices, giving the sequence 2, 3, 5, 17, 257, and 65537 (OEIS A092506).
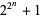 is a Fermat prime if and only if the period length of
is a Fermat prime if and only if the period length of 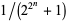 is equal to
is equal to 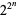 . In other words, Fermat primes are full reptend primes.
. In other words, Fermat primes are full reptend primes.
REFERENCES:
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.
Robinson, R. M. "Mersenne and Fermat Numbers." Proc. Amer. Math. Soc. 5, 842-846, 1954.
Sloane, N. J. A. Sequences A019434 and A092506 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|