


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-8-2020
Date: 11-8-2020
Date: 2-3-2020
|
In the original formulation, a quantity associated with ideal class groups. According to Chevalley's formulation, a Grössencharakter is a multiplicative character of the group of adèles that is trivial on the diagonally embedded 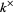 , where
, where 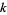 is a number field.
is a number field.
REFERENCES:
Hecke, E. "Eine neue Art von Zetafunktionen und ihre Beziehungen zur Verteilung der Primzahlen I." Math. Z. 1, 357-376, 1918.
Hecke, E. "Eine neue Art von Zetafunktionen und ihre Beziehungen zur Verteilung der Primzahlen II." Math. Z. 6, 11-51, 1920.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 24, 1980.
Knapp, A. W. "Group Representations and Harmonic Analysis, Part II." Not. Amer. Math. Soc. 43, 537-549, 1996.
Tate, J. "Fourier Analysis in Number Fields and Hecke's Zeta Functions." Ch. 15 in Algebraic Number Theory: Proceedings of an Instructional Conference Organized by the London Mathematical Society (Ed. J. W. S. Cassels and A. Fröhlich). New York: Academic Press, 1950.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|