


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-9-2020
Date: 5-1-2021
Date: 19-11-2020
|
The central binomial coefficient 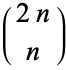 is never squarefree for
is never squarefree for 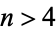 . This was proved true for all sufficiently large
. This was proved true for all sufficiently large 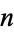 by Sárkőzy's theorem. Goetgheluck (1988) proved the conjecture true for
by Sárkőzy's theorem. Goetgheluck (1988) proved the conjecture true for 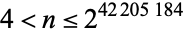 and Vardi (1991) for
and Vardi (1991) for 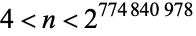 . The conjecture was proved true in its entirety by Granville and Ramare (1996).
. The conjecture was proved true in its entirety by Granville and Ramare (1996).
REFERENCES:
Erdős, P. and Graham, R. L. Old and New Problems and Results in Combinatorial Number Theory. Geneva, Switzerland: L'Enseignement Mathématique Université de Genève, Vol. 28, p. 71, 1980.
Goetgheluck, P. "Prime Divisors of Binomial Coefficients." Math. Comput. 51, 325-329, 1988.
Granville, A. and Ramare, O. "Explicit Bounds on Exponential Sums and the Scarcity of Squarefree Binomial Coefficients." Mathematika 43, 73-107, 1996.
Sander, J. W. "On Prime Divisors of Binomial Coefficients." Bull. London Math. Soc. 24, 140-142, 1992.
Sander, J. W. "A Story of Binomial Coefficients and Primes." Amer. Math. Monthly 102, 802-807, 1995.
Sárkőzy, A. "On Divisors of Binomial Coefficients. I." J. Number Th. 20, 70-80, 1985.
Vardi, I. "Applications to Binomial Coefficients." Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 25-28, 1991.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|