


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-3-2020
Date: 20-11-2019
Date: 2-5-2020
|
A Colbert number is any prime number with more than 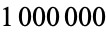 decimal digits whose discovery contributes to the long-sought after proof that
decimal digits whose discovery contributes to the long-sought after proof that 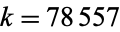 is the smallest Sierpiński number of the second kind. Colbert Numbers are named to honor Stephen T. Colbert.
is the smallest Sierpiński number of the second kind. Colbert Numbers are named to honor Stephen T. Colbert.
There are currently five known Colbert numbers, as summarized in the following table.
| Colbert number | decimal digits |
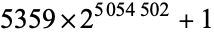 |
1521561 |
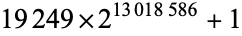 |
3918990 |
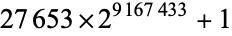 |
2759677 |
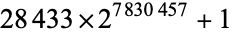 |
2357207 |
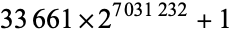 |
2116617 |
The Seventeen or Bust distributed computing effort is conducting a search for the remaining six Colbert numbers (where 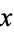 indicates the exponent is unknown).
indicates the exponent is unknown).
| unknown Colbert number | decimal digits |
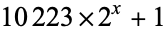 |
? |
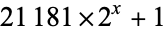 |
? |
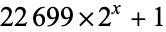 |
? |
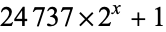 |
? |
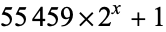 |
? |
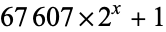 |
? |
REFERENCES:
Caldwell, C. "The Prime Glossary: Colbert Numbers". https://primes.utm.edu/glossary/xpage/ColbertNumber.html.
Helm, L.; Moore, P.; Samidoost, P.; and Woltman, G. "Resolution of the Mixed Sierpinski Problem." Integers: Elec. J. Combin. Numb. Th. 8, No. A61, 2008.
Helm, L. and Norris, D. "Seventeen or Bust: A Distributed Attack on the Sierpinski Problem." https://www.seventeenorbust.com/.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|