


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-5-2020
Date: 12-8-2020
Date: 19-8-2020
|

A perfect cuboid is a cuboid having integer side lengths, integer face diagonals
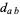 |
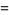 |
 |
(1) |
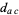 |
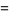 |
 |
(2) |
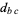 |
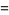 |
 |
(3) |
and an integer space diagonal
 |
(4) |
The problem of finding such a cuboid is also called the brick problem, diagonals problem, perfect box problem, perfect cuboid problem, or rational cuboid problem.
No perfect cuboids are known despite an exhaustive search for all "odd sides" up to 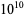 (Butler, pers. comm., Dec. 23, 2004).
(Butler, pers. comm., Dec. 23, 2004).
Solving the perfect cuboid problem is equivalent to solving the Diophantine equations
 |
 |
 |
(5) |
 |
 |
 |
(6) |
 |
 |
 |
(7) |
 |
 |
 |
(8) |
A solution with integer space diagonal and two out of three face diagonals is  ,
,  , and
, and  , giving
, giving  ,
,  ,
,  , and
, and  , which was known to Euler. A solution giving integer space and face diagonals with only a single nonintegral polyhedron edge is
, which was known to Euler. A solution giving integer space and face diagonals with only a single nonintegral polyhedron edge is  ,
,  , and
, and  , giving
, giving  ,
,  ,
,  , and
, and  .
.
REFERENCES:
Butler, B. "Durango Bill's The 'Integer Brick' Problem (The Euler Brick Problem)." https://www.durangobill.com/IntegerBrick.html.
Guy, R. K. "Is There a Perfect Cuboid? Four Squares whose Sums in Pairs are Square. Four Squares whose Differences are Square." §D18 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 173-181, 1994.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|