


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-10-2019
Date: 30-11-2020
Date: 17-12-2020
|
A 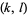 -multigrade equation is a Diophantine equation of the form
-multigrade equation is a Diophantine equation of the form
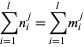 |
(1) |
for 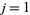 , ...,
, ..., 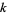 , where
, where 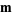 and
and 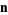 are
are 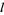 -vectors. Multigrade identities remain valid if a constant is added to each element of
-vectors. Multigrade identities remain valid if a constant is added to each element of 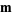 and
and 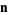 (Madachy 1979), so multigrades can always be put in a form where the minimum component of one of the vectors is 1.
(Madachy 1979), so multigrades can always be put in a form where the minimum component of one of the vectors is 1.
Moessner and Gloden (1944) give a bevy of multigrade equations. Small-order examples are the (2, 3)-multigrade with 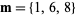 and
and 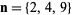 :
:
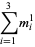 |
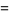 |
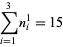 |
(2) |
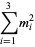 |
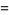 |
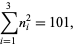 |
(3) |
the (3, 4)-multigrade with 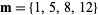 and
and 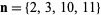 :
:
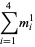 |
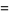 |
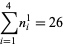 |
(4) |
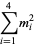 |
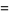 |
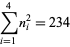 |
(5) |
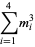 |
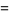 |
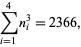 |
(6) |
and the (4, 6)-multigrade with 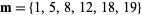 and
and 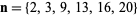 :
:
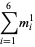 |
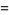 |
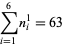 |
(7) |
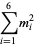 |
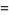 |
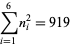 |
(8) |
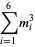 |
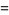 |
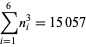 |
(9) |
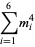 |
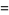 |
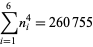 |
(10) |
(Madachy 1979).
A spectacular example with 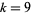 and
and 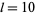 is given by
is given by 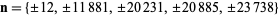 and
and 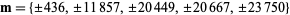 (Guy 1994), which has sums
(Guy 1994), which has sums
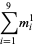 |
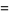 |
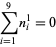 |
(11) |
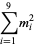 |
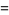 |
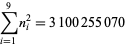 |
(12) |
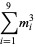 |
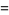 |
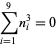 |
(13) |
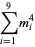 |
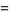 |
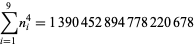 |
(14) |
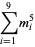 |
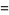 |
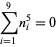 |
(15) |
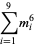 |
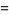 |
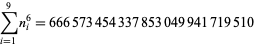 |
(16) |
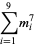 |
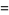 |
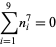 |
(17) |
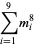 |
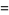 |
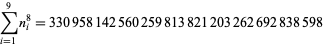 |
(18) |
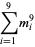 |
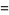 |
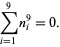 |
(19) |
Rivera considers multigrade equations involving primes, consecutive primes, etc.
Analogous multigrade identities to Ramanujan's fourth power identity of form
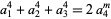 |
(20) |
can also be given for third and fifth powers, the former being
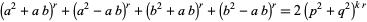 |
(21) |
with 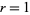 , 2, 3, for any positive integer
, 2, 3, for any positive integer 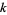 , and where
, and where
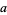 |
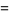 |
![1/2[(p-qi)^k+(p+qi)^k]](https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline77.gif) |
(22) |
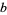 |
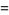 |
![1/2i[(p-qi)^k-(p+qi)^k]](https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline80.gif) |
(23) |
and the one for fifth powers
^n=2(p^2+pq+q^2)^(hn)](https://mathworld.wolfram.com/images/equations/MultigradeEquation/NumberedEquation4.gif) |
(24) |
for 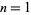 , 3, 5, any positive integer
, 3, 5, any positive integer 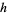 , and where
, and where
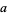 |
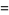 |
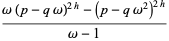 |
(25) |
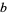 |
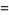 |
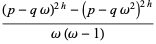 |
(26) |
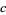 |
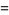 |
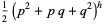 |
(27) |
with 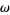 a complex cube root of unity and
a complex cube root of unity and 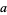 and
and 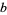 for both cases rational for arbitrary rationals
for both cases rational for arbitrary rationals 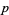 and
and 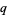 .
.
Multigrade sum-product identities as binary quadratic forms also exist for third, fourth, fifth powers. These are the second of the following pairs.
For third powers with 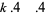 ,
,
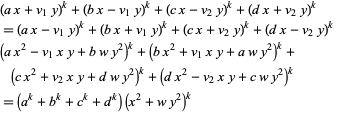 |
(28) |
for 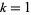 , 3,
, 3, 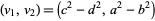 , and
, and 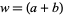 or
or 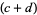 for arbitrary
for arbitrary 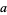 ,
, 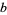 ,
, 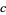 ,
, 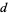 ,
,  , and
, and 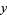 .
.
For fourth powers with 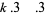 ,
,
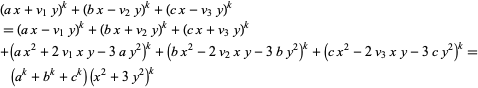 |
(29) |
for 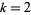 , 4,
, 4, 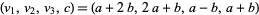 , for arbitrary
, for arbitrary 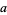 ,
, 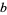 ,
,  ,
, 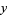 .
.
For fifth powers with 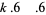 ,
,
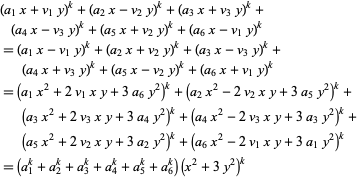 |
(30) |
for 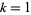 , 2, 3, 4, 5,
, 2, 3, 4, 5, 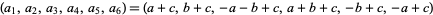 ,
, 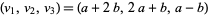 (which are the same
(which are the same 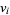 for fourth powers) for arbitrary
for fourth powers) for arbitrary 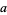 ,
, 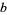 ,
, 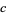 ,
,  ,
, 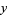 and one for seventh powers that uses
and one for seventh powers that uses 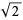 .
.
For seventh powers with 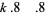 ,
,
 |
(31) |
for 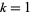 to 7,
to 7, 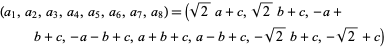 ,
, 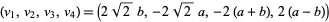 , for arbitrary,
, for arbitrary,  ,
,  ,
, 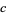 ,
,  ,
, 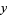 (Piezas 2006).
(Piezas 2006).
A multigrade 5-parameter binary quadratic form identity exists for 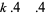 with
with 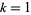 , 2, 3, 5. Given arbitrary variables
, 2, 3, 5. Given arbitrary variables 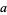 ,
, 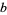 ,
, 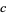 ,
,  ,
, 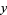 and defining
and defining 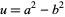 and
and 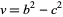 , then
, then
![[(-a+b+c)x^2+2(cu-bv)xy-(a+b+c)uvy^2]^k+[(a-b+c)x^2+2(cu+bv)xy+(a+b-c)uvy^2]^k+[(a+b-c)x^2+2(-cu-bv)xy+(a-b+c)uvy^2]^k+[-(a+b+c)x^2+2(-cu+bv)xy+(-a+b+c)uvy^2]^k-[-(a+b+c)x^2+2(-bu+av)xy+(a+b-c)uvy^2]^k-[(a+b-c)x^2+2(bu-av)xy-(a+b+c)uvy^2]^k-[(a-b+c)x^2+2(-bu-av)xy+(-a+b+c)uvy^2]^k-[(-a+b+c)x^2+2(bu+av)xy+(a-b+c)uvy^2]^k=0](https://mathworld.wolfram.com/images/equations/MultigradeEquation/NumberedEquation9.gif) |
(32) |
for 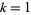 , 2, 3, 5 (T. Piezas, pers. comm., Apr. 27, 2006).
, 2, 3, 5 (T. Piezas, pers. comm., Apr. 27, 2006).
Chernick (1937) gave a multigrade binary quadratic form parametrization to 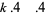 for
for 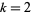 , 4, 6 given by
, 4, 6 given by
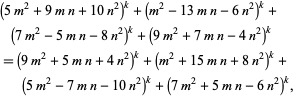 |
(33) |
an equation which depends on finding solutions to 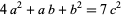 .
.
Sinha (1966ab) gave a multigrade binary quadratic form parametrization to 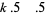 for
for 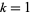 , 3, 5, 7 given by
, 3, 5, 7 given by
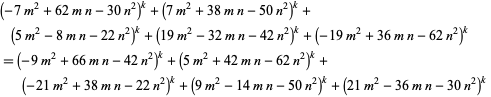 |
(34) |
which depended on solving the system 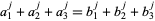 for
for 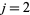 and 4 with
and 4 with 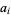 and
and 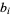 satisfying certain other conditions.
satisfying certain other conditions.
Sinha (1966ab), using a result of Letac, also gave a multigrade parametrization to 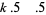 for
for 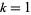 , 2, 4, 6, 8 given by
, 2, 4, 6, 8 given by
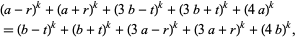 |
(35) |
where 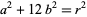 and
and 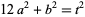 . One nontrivial solution can be given by
. One nontrivial solution can be given by 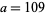 ,
, 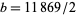 , and Sinha and Smyth proved in 1990 that there are an infinite number of distinct nontrivial solutions.
, and Sinha and Smyth proved in 1990 that there are an infinite number of distinct nontrivial solutions.
REFERENCES:
Chernick, J. "Ideal Solutions of the Tarry-Escott Problem." Amer. Math. Monthly 44, 62600633, 1937.
Gloden, A. Mehrgeradige Gleichungen. Groningen, Netherlands: Noordhoff, 1944.
Gloden, A. "Sur la multigrade 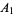 ,
, 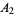 ,
, 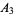 ,
, 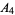 ,
, 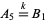 ,
, 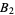 ,
, 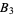 ,
, 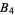 ,
, 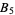 (
(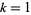 , 3, 5, 7)." Revista Euclides 8, 383-384, 1948.
, 3, 5, 7)." Revista Euclides 8, 383-384, 1948.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 143, 1994.
Kraitchik, M. "Multigrade." §3.10 in Mathematical Recreations. New York: W. W. Norton, p. 79, 1942.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 171-173, 1979.
Moessner, A. and Gloden, A. "Einige Zahlentheoretische Untersuchungen und Resultate." Bull. Sci. École Polytech. de Timisoara 11, 196-219, 1944.
Piezas, T. "Ramanujan and Fifth Power Identities." https://www.geocities.com/titus_piezas/Ramfifth.html.
Piezas, T. "Binary Quadratic Forms as Equal Sums of Like Powers." https://www.geocities.com/titus_piezas/Binary_quad.html.
Rivera, C. "Problems & Puzzles: Puzzle 065-Multigrade Relations." https://www.primepuzzles.net/puzzles/puzz_065.htm.
Sinha, T. "On the Tarry-Escott Problem." Amer. Math. Monthly 73, 280-285, 1966a.
Sinha, T. "Some System of Diophantine Equations of the Tarry-Escott Type." J. Indian Math. Soc. 30, 15-25, 1966b.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|