


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-1-2021
Date: 24-9-2020
Date: 17-8-2020
|
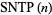 is the smallest prime such that
is the smallest prime such that 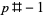 ,
, 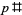 , or
, or 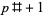 is divisible by
is divisible by 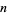 , where
, where 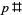 is the primorial of
is the primorial of 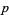 . Ashbacher (1996) shows that
. Ashbacher (1996) shows that 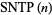 only exists
only exists
1. If there are no square or higher powers in the factorization of 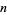 , or
, or
2. If there exists a prime 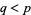 such that
such that 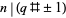 , where
, where 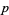 is the smallest power contained in the factorization of
is the smallest power contained in the factorization of 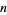 .
.
Therefore, 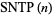 does not exist for the squareful numbers
does not exist for the squareful numbers 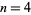 , 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, ... (OEIS A013929). The first few values of
, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, ... (OEIS A013929). The first few values of 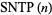 , where defined, are 2, 2, 2, 3, 3, 3, 5, 7, ... (OEIS A046026).
, where defined, are 2, 2, 2, 3, 3, 3, 5, 7, ... (OEIS A046026).
REFERENCES:
Ashbacher, C. "A Note on the Smarandache Near-To-Primordial Function." Smarandache Notions J. 7, 46-49, 1996.
Mudge, M. R. "The Smarandache Near-To-Primorial Function." Abstracts of Papers Presented to the Amer. Math. Soc. 17, 585, 1996.
Sloane, N. J. A. Sequences A013929 and A046026 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|