Tetrahedron Tetrahedron Picking

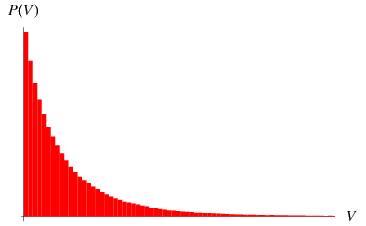
The mean tetrahedron volume of a tetrahedron with vertices chosen at random inside another tetrahedron of unit volume is given by

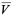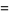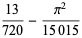			(1)
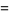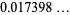			(2)

(OEIS A093525; Buchta and Reitzner 1992; Mannion 1994; Schneider 1997, p. 170; Buchta and Reitzner 2001; Zinani 2003).

This provides a disproof of the conjecture that the solution to this problem is a rational number (1/57 had been suggested by Croft et al. 1991, p. 54), and renders obsolete Solomon's statement that "Explicit values for random points in non-spherical regions such as tetrahedrons, parallelepipeds, etc., have apparently not yet been successfully calculated" (Solomon 1978, p. 124).

Furthermore, Buchta and Reitzner (2001) give an explicit formula for the expected volume of the convex hull of 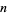 points chosen at random in a three-dimensional simplex for arbitrary .

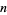REFERENCES:

Blaschke, W. "Über affine Geometrie XI: Lösung des 'Vierpunktproblems' von Sylvester aus der Theorie der geometrischen Wahrscheinlichkeiten." Ber. Verh. Sachs. Akad. Wiss. Leipzig Math.-Phys. Kl. 69, 436-453, 1917.

Buchta, C. and Reitzner, M. "What Is the Expected Volume of a Tetrahedron whose Vertices are Chosen at Random from a Given Tetrahedron." Anz. Österreich. Akad. Wiss. Math.-Natur. Kl. 129, 63-68, 1992.

Buchta, C. and Reitzner, M. "The Convex Hull of Random Points in a Tetrahedron: Solution of Blaschke's Problem and More General Results." J. reine angew. Math. 536, 1-29, 2001.

Croft, H. T.; Falconer, K. J.; and Guy, R. K. "Random Polygons and Polyhedra." §B5 in Unsolved Problems in Geometry. New York: Springer-Verlag, pp. 54-57, 1991.

Do, K.-A. and Solomon, H. "A Simulation Study of Sylvester's Problem in Three Dimensions." J. Appl. Prob. 23, 509-513, 1986.

Klee, V. "What is the Expected Volume of a Simplex Whose Vertices are Chosen at Random from a Given Convex Body." Amer. Math. Monthly 76, 286-288, 1969.

Mannion, D. "The Volume of a Tetrahedron Whose Vertices Are Chosen at Random in the Interior of a Parent Tetrahedron." Adv. Appl. Prob. 26, 577-596, 1994.

Schneider, R. "Discrete Aspects of Stochastic Geometry." Ch. 9 in Handbook of Discrete and Computational Geometry (Ed. J. E. Goodman and J. O'Rourke). Boca Raton, FL: CRC Press, pp. 167-184, 1997.

Sloane, N. J. A. Sequence A093525 in "The On-Line Encyclopedia of Integer Sequences."

Solomon, H. Geometric Probability. Philadelphia, PA: SIAM, p. 124, 1978.

Zinani, A. "The Expected Volume of a Tetrahedron Whose Vertices are Chosen at Random in the Interior of a Cube." Monatshefte Math. 139, 341-348, 2003.