


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2020
Date: 23-1-2021
Date: 20-2-2020
|
Given a simplex of unit content in Euclidean 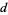 -space, pick
-space, pick 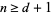 points uniformly and independently at random, and denote the expected content of their convex hull by
points uniformly and independently at random, and denote the expected content of their convex hull by 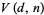 . Exact values are known only for
. Exact values are known only for 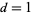 and 2.
and 2.
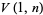 |
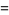 |
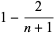 |
(1) |
 |
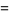 |
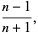 |
(2) |
(Buchta 1984, 1986), giving the first few values 0, 1/3, 1/2, 3/5, 2/3, 5/7, ... (OEIS A026741 and A026741).
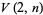 |
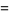 |
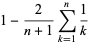 |
(3) |
 |
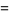 |
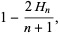 |
(4) |
where 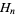 is a harmonic number (Buchta 1984, 1986), giving the first few values 0, 0, 1/12, 1/6, 43/180, 3/10, 197/560, 499/1260, ... (OEIS A093762 and A093763).
is a harmonic number (Buchta 1984, 1986), giving the first few values 0, 0, 1/12, 1/6, 43/180, 3/10, 197/560, 499/1260, ... (OEIS A093762 and A093763).
Not much is known about 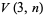 , although
, although
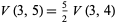 |
(5) |
(Buchta 1983, 1986) and
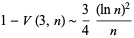 |
(6) |
(Buchta 1986).
Furthermore, Buchta and Reitzner (2001) give an explicit formula for the expected volume of the convex hull of 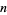 points chosen at random in a three-dimensional simplex for arbitrary
points chosen at random in a three-dimensional simplex for arbitrary 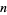 .
.
REFERENCES:
Buchta, C. "Über die konvexe Hülle von Zufallspunkten in Eibereichen." Elem. Math. 38, 153-156, 1983.
Buchta, C. "Zufallspolygone in konvexen Vielecken." J. reine angew. Math. 347, 212-220, 1984.
Buchta, C. "A Note on the Volume of a Random Polytope in a Tetrahedron." Ill. J. Math. 30, 653-659, 1986.
Buchta, C. and Reitzner, M. "What Is the Expected Volume of a Tetrahedron whose Vertices are Chosen at Random from a Given Tetrahedron." Anz. Österreich. Akad. Wiss. Math.-Natur. Kl. 129, 63-68, 1992.
Buchta, C. and Reitzner, M. "The Convex Hull of Random Points in a Tetrahedron: Solution of Blaschke's Problem and More General Results." J. reine angew. Math. 536, 1-29, 2001.
Klee, V. "What is the Expected Volume of a Simplex whose Vertices are Chosen at Random from a Given Convex Body." Amer. Math. Monthly 76, 286-288, 1969.
Sloane, N. J. A. Sequences A026741, A093762, and A093763 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|