
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-7-2020
Date: 15-11-2020
Date: 30-12-2020
|
An integer 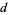 is a fundamental discriminant if it is not equal to 1, not divisible by any square of any odd prime, and satisfies
is a fundamental discriminant if it is not equal to 1, not divisible by any square of any odd prime, and satisfies 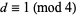 or
or 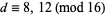 . The function FundamentalDiscriminantQ[d] in the Wolfram Language version 5.2 add-on package NumberTheory`NumberTheoryFunctions` tests if an integer
. The function FundamentalDiscriminantQ[d] in the Wolfram Language version 5.2 add-on package NumberTheory`NumberTheoryFunctions` tests if an integer 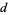 is a fundamental discriminant.
is a fundamental discriminant.
It can be implemented as:
FundamentalDiscriminantQ[n_Integer] := n != 1&&
(Mod[n, 4] == 1 [Or]
! Unequal[Mod[n, 16], 8, 12])&&
SquareFreeQ[n/2^IntegerExponent[n, 2]]
The first few positive fundamental discriminants are 5, 8, 12, 13, 17, 21, 24, 28, 29, 33, ... (OEIS A003658). Similarly, the first few negative fundamental discriminants are 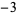 ,
, 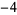 ,
, 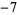 ,
, 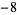 ,
, 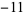 ,
, 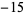 ,
, 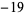 ,
, 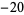 ,
, 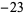 ,
, 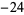 ,
, 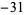 , ... (OEIS A003657).
, ... (OEIS A003657).
REFERENCES:
Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Math. Comput. 61, 29-68, 1993.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, p. 294, 1987.
Cohn, H. Advanced Number Theory. New York: Dover, 1980.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, 2005a.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, 2005b.
Dickson, L. E. History of the Theory of Numbers, Vol. 3: Quadratic and Higher Forms. New York: Dover, 2005c.
Sloane, N. J. A. Sequences A003657/M2332 and A003658/M3776 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|