Rabbit Sequence

A sequence which arises in the hypothetical reproduction of a population of rabbits. Let the substitution system map 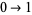 correspond to young rabbits growing old, and  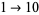correspond to old rabbits producing young rabbits. Starting with 0 and iterating using string rewriting gives the terms 1, 10, 101, 10110, 10110101, 1011010110110, .... A recurrence plot of the limiting value of this sequence is illustrated above.

Converted to decimal, this sequence gives 1, 2, 5, 22, 181, ... (OEIS A005203), with the 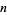th term given by the recurrence relation

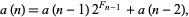with 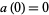, , 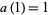and 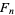 the 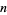th Fibonacci number.

The limiting sequence written as a binary fraction 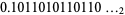 (OEIS A005614), where  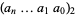denotes a binary number (i.e., a number written in base 2, so  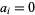or 1), is called the rabbit constant.

REFERENCES:

Davison, J. L. "A Series and Its Associated Continued Fraction." Proc. Amer. Math. Soc. 63, 29-32, 1977.

Gould, H. W.; Kim, J. B.; and Hoggatt, V. E. Jr. "Sequences Associated with t-ary Coding of Fibonacci's Rabbits." Fib. Quart. 15, 311-318, 1977.

Schroeder, M. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, p. 55, 1991.

Sloane, N. J. A. Sequences A005203/M1539 and A005614 in "The On-Line Encyclopedia of Integer Sequences."