


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-11-2019
Date: 30-7-2020
Date: 28-1-2021
|
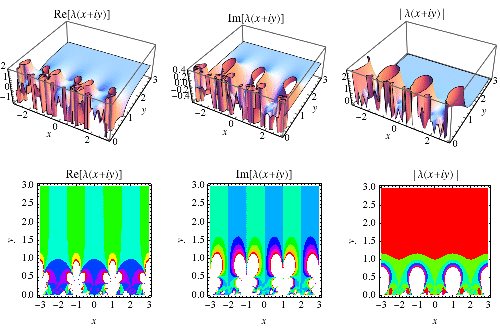 |
The elliptic lambda function 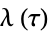 is a
is a 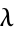 -modular function defined on the upper half-plane by
-modular function defined on the upper half-plane by
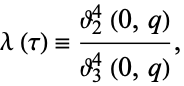 |
(1) |
where 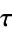 is the half-period ratio,
is the half-period ratio, 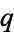 is the nome
is the nome
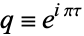 |
(2) |
and 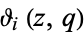 are Jacobi theta functions.
are Jacobi theta functions.
The elliptic lambda function is essentially the same as the inverse nome, the difference being that elliptic lambda function is a function of the half-period ratio 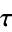 , while the inverse nome is a function of the nome
, while the inverse nome is a function of the nome 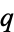 , where
, where 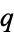 is itself a function of
is itself a function of 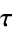 .
.
It is implemented as the Wolfram Language function ModularLambda[tau].
The elliptic lambda function 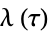 satisfies the functional equations
satisfies the functional equations
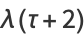 |
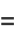 |
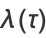 |
(3) |
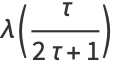 |
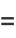 |
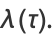 |
(4) |
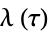 has the series expansion
has the series expansion
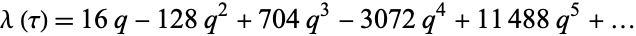 |
(5) |
(OEIS A115977), and 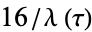 has the series expansion
has the series expansion
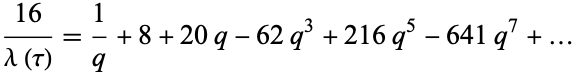 |
(6) |
(OEIS A029845; Conway and Norton 1979; Borwein and Borwein 1987, p. 117).
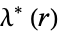 gives the value of the elliptic modulus
gives the value of the elliptic modulus 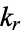 for which the complementary
for which the complementary 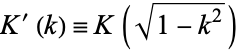 and normal complete elliptic integrals of the first kind
and normal complete elliptic integrals of the first kind 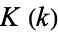 are related by
are related by
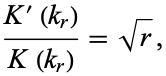 |
(7) |
i.e., the elliptic integral singular value for 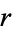 . It can be computed from
. It can be computed from
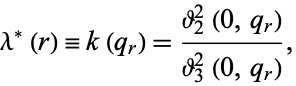 |
(8) |
where
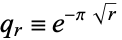 |
(9) |
and 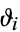 is a Jacobi theta function.
is a Jacobi theta function. 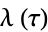 is related to
is related to 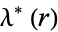 by
by
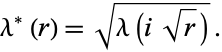 |
(10) |
For all rational 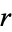 ,
, 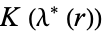 and
and 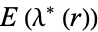 are known as elliptic integral singular values, and can be expressed in terms of a finite number of gamma functions (Selberg and Chowla 1967). Values of
are known as elliptic integral singular values, and can be expressed in terms of a finite number of gamma functions (Selberg and Chowla 1967). Values of 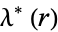 for small
for small 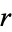 include
include
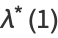 |
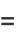 |
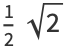 |
(11) |
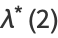 |
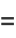 |
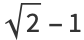 |
(12) |
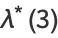 |
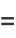 |
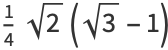 |
(13) |
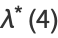 |
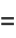 |
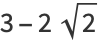 |
(14) |
 |
 |
 |
(15) |
 |
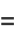 |
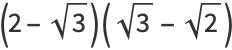 |
(16) |
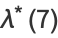 |
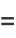 |
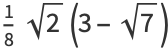 |
(17) |
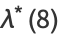 |
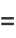 |
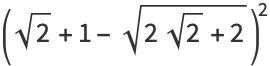 |
(18) |
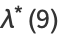 |
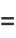 |
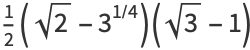 |
(19) |
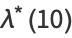 |
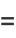 |
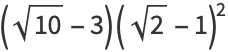 |
(20) |
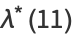 |
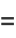 |
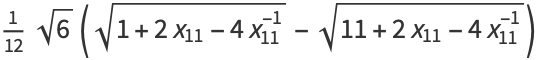 |
(21) |
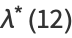 |
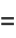 |
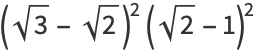 |
(22) |
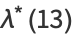 |
 |
 |
(23) |
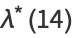 |
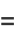 |
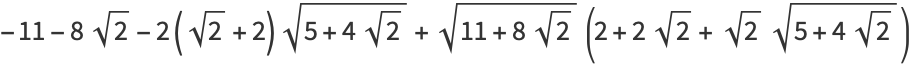 |
(24) |
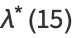 |
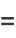 |
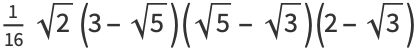 |
(25) |
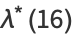 |
 |
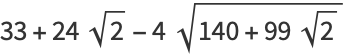 |
(26) |
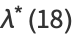 |
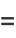 |
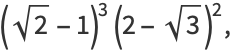 |
(27) |
where
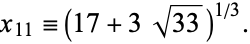 |
(28) |
The algebraic orders of these are given by 2, 2, 4, 2, 8, 4, 4, 4, 8, 4, 12, 4, 8, 8, 8, 4, ... (OEIS A084540).
Some additional exact values are given by
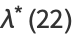 |
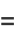 |
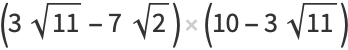 |
(29) |
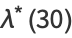 |
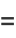 |
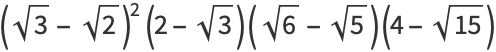 |
(30) |
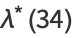 |
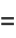 |
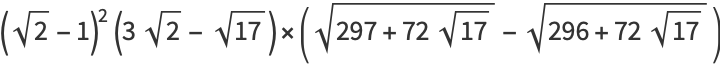 |
(31) |
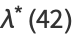 |
 |
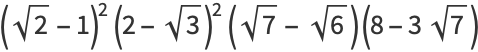 |
(32) |
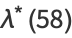 |
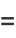 |
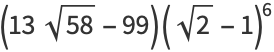 |
(33) |
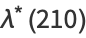 |
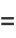 |
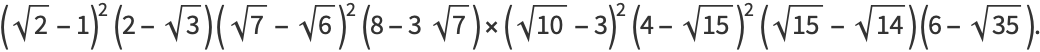 |
(34) |
Exact values can also be found for rational  , including
, including
 |
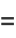 |
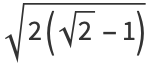 |
(35) |
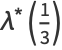 |
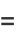 |
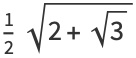 |
(36) |
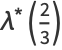 |
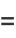 |
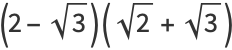 |
(37) |
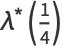 |
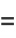 |
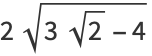 |
(38) |
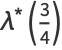 |
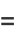 |
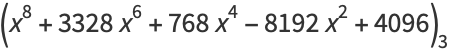 |
(39) |
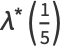 |
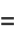 |
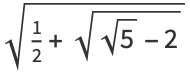 |
(40) |
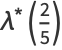 |
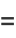 |
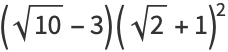 |
(41) |
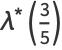 |
 |
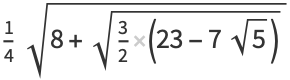 |
(42) |
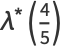 |
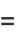 |
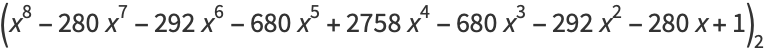 |
(43) |
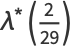 |
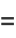 |
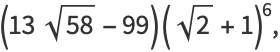 |
(44) |
where 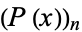 is a polynomial root.
is a polynomial root.
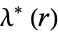 is related to the Ramanujan g- and G-functions by
is related to the Ramanujan g- and G-functions by
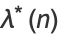 |
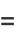 |
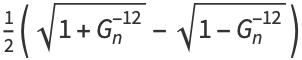 |
(45) |
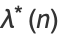 |
 |
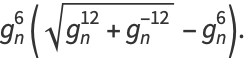 |
(46) |
REFERENCES:
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 139 and 298, 1987.
Bowman, F. Introduction to Elliptic Functions, with Applications. New York: Dover, pp. 75, 95, and 98, 1961.
Conway, J. H. and Norton, S. P. "Monstrous Moonshine." Bull. London Math. Soc. 11, 308-339, 1979.
Selberg, A. and Chowla, S. "On Epstein's Zeta-Function." J. reine angew. Math. 227, 86-110, 1967.
Sloane, N. J. A. Sequences A029845, A084540, and A115977 in "The On-Line Encyclopedia of Integer Sequences."
Watson, G. N. "Some Singular Moduli (1)." Quart. J. Math. 3, 81-98, 1932.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|