المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Pippenger Product |
 554
 11:35 صباحاً
date: 18-11-2019 |
Author : Pippenger, N 
Book or Source : "An Infinite Product for e." Amer. Math. Monthly 87 
Page and Part : ...|
Read More
Date: 1-10-2020
511
Date: 14-9-2020
529
Date: 17-11-2020
704
|
The Pippenger product is an unexpected Wallis-like formula for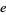 
given by
 |
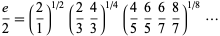(1) |
(OEIS A084148 and A084149; Pippenger 1980). Here, the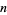 
th term for 
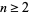is given by
 |
 |
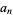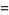![([(2^(n-1)-1)!!]^2[(2^n)!!]^2)/(2[(2^(n-1))!!]^2[(2^n-1)!!]^2)](http://mathworld.wolfram.com/images/equations/PippengerProduct/Inline6.gif) |
(2) |
 |
 |
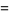![(2^(2^n-1)[Gamma(1/2+2^(n-2))]^4)/(pi[Gamma(1/2+2^(n-1))]^2),](http://mathworld.wolfram.com/images/equations/PippengerProduct/Inline9.gif) |
(3) |
where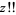 
is a double factorial and 
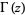is the gamma function.
REFERENCES:
Pippenger, N. "An Infinite Product for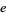 
." Amer. Math. Monthly 87, 391, 1980.
Sloane, N. J. A. Sequences A084148 and A084149 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
